
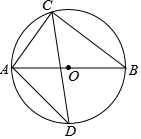
 如圖,⊙O的直徑為AB,弦AC長為6,BC長為8,∠ACB的平分線交⊙O于D,則弦AD的長為( )
如圖,⊙O的直徑為AB,弦AC長為6,BC長為8,∠ACB的平分線交⊙O于D,則弦AD的長為( )| A. | 5$\sqrt{2}$ | B. | 7 | C. | 8$\sqrt{2}$ | D. | 9 |
分析 先根據圓周角定理得出∠ACB=90°,由勾股定理求出AB的長,連接BD,易得△ABD是等腰直角三角形,然后由特殊角的三角函數值,求得AD的長.
解答 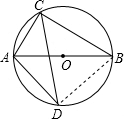 解:∵⊙O的直徑為AB,
解:∵⊙O的直徑為AB,
∴∠ACB=90°.
∵AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
連接BD,
∵AB是⊙O的直徑,
∴∠ACB=∠ADB=90°,
∵CD是∠ACB的平分線,
∴∠ACD=$\frac{1}{2}$∠ACB=45°,
∴∠ABD=∠ACD=45°,
∴AD=BD,
∵AB=10,
∴AD=AB•sin45°=5$\sqrt{2}$.
故選A.
點評 此題考查了圓周角定理、等腰直角三角形的性質及勾股定理,此題難度不大,注意掌握輔助線的作法,注意數形結合思想的應用.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
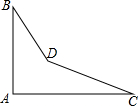 如圖,是一個零件的形狀,按規定∠A應等于90°,∠B與∠C分別是32°和27°,檢測工人量得∠BDC=150°,問該零件是否合格?為什么?
如圖,是一個零件的形狀,按規定∠A應等于90°,∠B與∠C分別是32°和27°,檢測工人量得∠BDC=150°,問該零件是否合格?為什么?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com