Question

10．寧波軌道交通4號線已開工建設，計劃2020年通車試運營．為了了解鎮民對4號線地鐵票的定價意向，某鎮某校數學興趣小組開展了“你認為寧波4號地鐵起步價定為多少合適”的問卷調查，并將調查結果整理后制成了如下統計圖，根據圖中所給出的信息解答下列問題：
（1）求本次調查中該興趣小組隨機調查的人數；
（2）請你把條形統計圖補充完整；
（3）如果在該鎮隨機咨詢一位居民，那么該居民支持“起步價為2元或3元”的概率是$\frac{4}{5}$
（4）假設該鎮有3萬人，請估計該鎮支持“起步價為3元”的居民大約有多少人？

Answer 1

分析 （1）根據5元在扇形統計圖中的圓心角和人數可以解答本題；
（2）根據（1）中的答案和統計圖中的數據可以求得條形統計圖中的未知數據，從而可以將條形統計圖補種完整；
（3）根據統計圖中的數據可以得到該居民支持“起步價為2元或3元”的概率；
（4）根據前面求得的數據可以估計該鎮支持“起步價為3元”的居民人數．

解答 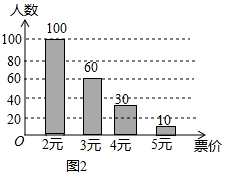解：（1）由題意可得，
同意定價為5元的所占的百分比為：18°÷360°×100%=5%，
∴本次調查中該興趣小組隨機調查的人數為：10÷5%=200（人），
即本次調查中該興趣小組隨機調查的人數有200人；
（2）由題意可得，
2元的有：200×50%=100人，
3元的有：200-100-30-10=60人，
補全的條形統計圖如右圖所示；
（3）由題意可得，
該居民支持“起步價為2元或3元”的概率是：$\frac{100+60}{200}=\frac{4}{5}$，
故答案為：$\frac{4}{5}$；
（4）由題意可得，
$30000×\frac{60}{200}=9000$（人），
即該鎮支持“起步價為3元”的居民大約有9000人．

點評 本題考查條形統計圖、扇形統計圖、用樣本估計總體、概率公式，解答本題的關鍵是明確題意，找出所求問題需要的條件，利用數形結合的思想解答問題，注意第（2）問中是求2元和3元的概率，不要誤認為求3元和4元的．