Question

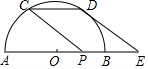
10．如圖，已知半圓O的直徑AB為8，P為OB的中點，C為半圓上一點，連結CP，若將CP沿射線AB方向平移至DE，若DE恰好與⊙O相切于點D，則平移的距離為$\sqrt{33}$-1．

Answer 1

分析 如圖，過OM⊥CD于M，連接OD，則CM=DM，由DE是⊙O的切線，得到OD⊥DE，由平移的性質得到CD∥PE，CD=PE，根據平行線的性質得到∠1=∠2，根據相似三角形的性質即可得到結論．

解答 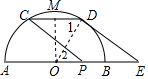解：如圖，過OM⊥CD于M，連接OD，
則CM=DM，
∵DE是⊙O的切線，
∴OD⊥DE，
∵將CP沿射線AB方向平移至DE，
∴CD∥PE，CD=PE，
∴∠1=∠2，
∵∠DMO=∠ODE=90°，
∴△DMO∽△ODE，
∴$\frac{MO}{OD}=\frac{OD}{OE}$，
設CD=x，
∴$\frac{\frac{1}{2}x}{4}$=$\frac{4}{x+2}$，
∴x=$\sqrt{33}$-1，
∴平移的距離為$\sqrt{33}$-1．
故答案為：$\sqrt{33}$-1．

點評 本題考查了切線的性質，平移的性質，相似三角形的判定和性質，掌握的作出輔助線是解題的關鍵．