
| x | … | -1 | 0 | 3 | … |
| y | … | 0 | 3/2 | 0 | … |
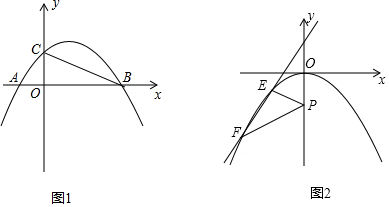
分析 (1)由拋物線y=-$\frac{1}{2}$x2+bx+c與x軸交于A、B兩點,(-1,0),(3,0),即可求得拋物線的解析式;
(2)首先取OB的中點P($\frac{3}{2}$,0),連接CP,然后過點P作PQ∥BC交拋物線于Q,即為所求;首先求得直線BC的解析式,然后由平行線的性質,求得直線PQ的解析式,再聯立$\left\{\begin{array}{l}{y=-\frac{1}{2}x+\frac{3}{4}}\\{y=-\frac{1}{2}{x}^{2}+x+\frac{3}{2}}\end{array}\right.$,即可求得答案;
(3)首先得到平移后的拋物線的解析式為:y=-$\frac{1}{2}$x2,再過點E作EM⊥y軸于M,過點F作FN⊥y軸于N,易得Rt△EPM∽Rt△FPN,再聯立$\left\{\begin{array}{l}{y=kx+b}\\{y=-\frac{1}{2}{x}^{2}}\end{array}\right.$,即可求得答案.
解答 解:(1)∵拋物線y=-$\frac{1}{2}$x2+bx+c與x軸交于A、B兩點,(-1,0),(3,0),
∴y=-$\frac{1}{2}$(x+1)(x-3),
∴拋物線的解析式為:y=-$\frac{1}{2}$x2+x+$\frac{3}{2}$; (2)取OB的中點P($\frac{3}{2}$,0),連接CP,
(2)取OB的中點P($\frac{3}{2}$,0),連接CP,
則S△PBC=$\frac{1}{2}$S△BOC,
過點P作PQ∥BC交拋物線于Q,即為所求;
∵拋物線與y軸交于點C,
∴點C的坐標為:(0,$\frac{3}{2}$),
設直線BC的解析式為y=kx+b,
$\left\{\begin{array}{l}{b=\frac{3}{2}}\\{3k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴直線BC的解析式為y=-$\frac{1}{2}$x+$\frac{3}{2}$,
∴設直線PQ的解析式為y=-$\frac{1}{2}$x+n,
∴-$\frac{1}{2}$×$\frac{3}{2}$+n=0,
∴n=$\frac{3}{4}$,
∴直線PQ的解析式為y=-$\frac{1}{2}$x+$\frac{3}{4}$,
聯立$\left\{\begin{array}{l}{y=-\frac{1}{2}x+\frac{3}{4}}\\{y=-\frac{1}{2}{x}^{2}+x+\frac{3}{2}}\end{array}\right.$,
解得:x=$\frac{-3±\sqrt{3}}{2}$,
若S△BCQ≥$\frac{1}{2}$S△BOC
則xQ的取值范圍為:xQ≥$\frac{-3+\sqrt{3}}{2}$或xQ≤$\frac{-3-\sqrt{3}}{2}$; (3)平移后的拋物線的解析式為:y=-$\frac{1}{2}$x2,
(3)平移后的拋物線的解析式為:y=-$\frac{1}{2}$x2,
過點E作EM⊥y軸于M,過點F作FN⊥y軸于N,
由反射可知:∠EPM=∠FPN,
∴Rt△EPM∽Rt△FPN,
∴$\frac{KM}{FN}$=$\frac{PM}{PN}$,
設E(x1,y1)、F(x2,y2),設直線EF的解析式為y=kx+b,
∴$\frac{-{x}_{1}}{-{x}_{2}}$=$\frac{{y}_{1}+1}{-1-{y}_{2}}$,
∴x1(1+y2)+x2(y1+1)=0,
聯立$\left\{\begin{array}{l}{y=kx+b}\\{y=-\frac{1}{2}{x}^{2}}\end{array}\right.$,
整理得x2+2kx+2b=0,
∴x1+x2=-2k,x1x2=2b,
∵x1(1+y2)+x2(y1+1)=x1(1+kx2+b)+x2(kx1+b+1)=0,
∴2bx1x2+(b+1)(x1+x2)=0,
∴2kb-2k=0,b=1,
∴直線EF的解析式為y=kx+1
∴直線EF的過定點(0,1).
點評 此題屬于二次函數的綜合題.考查了相似三角形的判定與性質、待定系數法求函數的解析式以及函數的交點問題.注意準確作出輔助線是解此題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:填空題
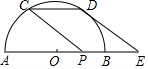 如圖,已知半圓O的直徑AB為8,P為OB的中點,C為半圓上一點,連結CP,若將CP沿射線AB方向平移至DE,若DE恰好與⊙O相切于點D,則平移的距離為$\sqrt{33}$-1.
如圖,已知半圓O的直徑AB為8,P為OB的中點,C為半圓上一點,連結CP,若將CP沿射線AB方向平移至DE,若DE恰好與⊙O相切于點D,則平移的距離為$\sqrt{33}$-1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com