
分析 設這杯飲料為1,根據題意得第一次后剩下飲料是原來的1-$\frac{1}{2}$=$\frac{1}{2}$,第二次后剩下飲料是原來的1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)=(1-$\frac{1}{2}$)2=$\frac{1}{4}$,第三次后剩下飲料是原來的(1-$\frac{1}{2}$)$\frac{1}{2}$(1-$\frac{1}{2}$)-$\frac{1}{2}$[1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)]=(1-$\frac{1}{2}$)3=$\frac{1}{8}$,由此發現規律,寫出第,四次和第n次的結果.
解答 解:設這杯飲料為1,根據題意得
第一次后剩下飲料是原來的:1-$\frac{1}{2}$=$\frac{1}{2}$,
第二次后剩下飲料是原來的:1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)=(1-$\frac{1}{2}$)2=$\frac{1}{4}$,
第三次后剩下飲料是原來的:(1-$\frac{1}{2}$)$\frac{1}{2}$(1-$\frac{1}{2}$)-$\frac{1}{2}$[1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)]=(1-$\frac{1}{2}$)3=$\frac{1}{8}$,
∴第n次后剩下飲料是原來的:(1-$\frac{1}{2}$)n=$\frac{1}{{2}^{n}}$,
故答案為:$\frac{1}{{2}^{n}}$.
點評 本題主要考查數字的變化規律,根據題意分別計算出第一、二、三次剩余的飲料是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
 如圖是用相同的正方形磚鋪成的地面,一寶物藏在其中某一塊磚的下面,則寶物在白色區域的概率是( )
如圖是用相同的正方形磚鋪成的地面,一寶物藏在其中某一塊磚的下面,則寶物在白色區域的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{15}$ | D. | $\frac{8}{15}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2006 | B. | 2014 | C. | 2015 | D. | 2016 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
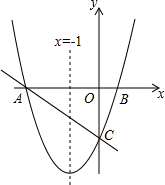 如圖,對稱軸為直線x=-1的拋物線y=x2+bx+c與x軸相交于A,B兩點,其中點A的坐標為(-3,0),點C為拋物線與y軸的交點.
如圖,對稱軸為直線x=-1的拋物線y=x2+bx+c與x軸相交于A,B兩點,其中點A的坐標為(-3,0),點C為拋物線與y軸的交點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com