
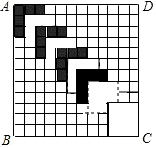
 如圖,正方形ABCD的邊長為12,劃分成12×12個小正方形格.將邊長為n(n為整數,且2≤n≤11)的黑白兩色正方形紙片按圖中的方式黑白相間地擺放,第一張n×n的紙片正好蓋住正方形ABCD左上角的n×n個小正方形格,第二張紙片蓋住第一張紙片的部分恰好為(n-1)×(n-1)的正方形.如此擺放下去,最后直到紙片蓋住正方形ABCD的右下角為止.請你認真觀察思考后回答下列問題:
如圖,正方形ABCD的邊長為12,劃分成12×12個小正方形格.將邊長為n(n為整數,且2≤n≤11)的黑白兩色正方形紙片按圖中的方式黑白相間地擺放,第一張n×n的紙片正好蓋住正方形ABCD左上角的n×n個小正方形格,第二張紙片蓋住第一張紙片的部分恰好為(n-1)×(n-1)的正方形.如此擺放下去,最后直到紙片蓋住正方形ABCD的右下角為止.請你認真觀察思考后回答下列問題:分析 (1)根據題意,可得應蓋住正方形ABCD的對角線上的12個格.當是邊長為2的紙片時,則需要1+(12-2)=11張紙片.
(2)①第一個面積為n2,第二個為一個包邊,共有12-n個,每個由2n-1個小正方形構成,包邊的總面積為(12-n)×(2n-1),由此得出S1=(12-n)×(2n-1)+n2;S2=144-(12-n)×(2n-1)-n2,代入計算得出答案即可;
②由①得出答案即可.
解答 解:(1)根據題意可得,應蓋住正方形ABCD的對角線上的12個格.當是邊長為2的紙片時,則需要1+(12-2)=11張紙片.
故答案為:11;
(2)第一個面積為n2,第二個為一個包邊,共有12-n個,每個由2n-1個小正方形構成,包邊的總面積為(12-n)×(2n-1)
∴①S1=10×3+4=34,S2=144-34=110.
∴S1:S2的值是34:110=17:55.
②根據題意,得S1=(12-n)×(2n-1)+n2;S2=144-(12-n)×(2n-1)-n2,
若S1=S2時,(12-n)×(2n-1)+n2=144-(12-n)×(2n-1)-n2,
整理得,則n=4或21.
∵2≤n≤11,
∴n=21舍去,
故n=4.
點評 本題考查圖形的變化規律及整式的運算和解方程的能力,找出被紙片蓋住的面積和未被蓋住的面積,變化的規律是解決問題的關鍵.


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
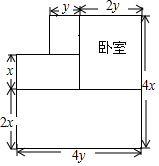 如圖,是張老師買的經濟適用房平面結構示意圖,圖中標明了有關尺寸(墻體厚度忽略不計,單位:m),房主計劃把臥室以外的地面都鋪上地磚,
如圖,是張老師買的經濟適用房平面結構示意圖,圖中標明了有關尺寸(墻體厚度忽略不計,單位:m),房主計劃把臥室以外的地面都鋪上地磚,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
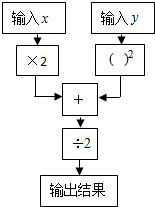 求代數式的值:
求代數式的值:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com