
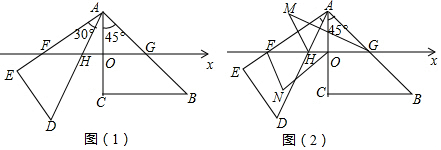
分析 (1)由于∠OCB=90°,則OG=OA=4,再根據三角形面積公式可計算出GH=5,FH=4,所以OH=1,OF=5,所以點F對應的數軸上的數是-5,點H對應的數軸上的數是-1;
(2)由∠AHF的平分線和∠AGH的平分線交于點M得到∠FHM=$\frac{1}{2}$∠FHA,∠HGM=$\frac{1}{2}$∠HGA,根據三角形外角性質得∠FHM=∠M+∠HGM,∠FHA=∠HGA+∠HAG,則2∠M+2∠HGM=∠HGA+∠HAG,所以∠M=$\frac{1}{2}$∠HAG=$\frac{1}{2}$(∠HAO+∠OAG)=$\frac{1}{2}$α+22.5°;
(3)根據(2)中證明方法,可得到∠N=90°-$\frac{1}{2}$∠FAO=90°-$\frac{1}{2}$∠FAH-$\frac{1}{2}$∠OAH=90°-15°-$\frac{1}{2}$∠OAH=75°-$\frac{1}{2}$∠OAH,再根據∠M=$\frac{1}{2}$∠OAH+22.5°,即可得到∠M+∠N=97.5°.
解答 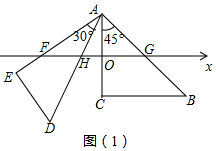 解:(1)如圖1,∵AC的中點過數軸的原點O,AC=8,
解:(1)如圖1,∵AC的中點過數軸的原點O,AC=8,
∴AO=4,
∵△AGH的面積是10,
∴$\frac{1}{2}$×4×GH=10,
解得GH=5,
又∵∠AOG=90°,∠OAG=45°,
∴OG=OA=4,
∴OH=1,
∴點H對應的數軸上的數是-1,
∵△AHF的面積是8,
∴$\frac{1}{2}$FH•4=8,
解得FH=4,
∴OF=OH+FH=5,
∴點F對應的數軸上的數是-5,
故答案為:-5,-1;
(2)如圖2,∵∠AHF的平分線和∠AGH的平分線交于點M,
∴∠FHM=$\frac{1}{2}$∠FHA,∠HGM=$\frac{1}{2}$∠HGA,
∵∠FHM=∠M+∠HGM,∠FHA=∠HGA+∠HAG,
∴2∠M+2∠HGM=∠HGA+∠HAG,即2∠M=∠HAG,
∴∠M=$\frac{1}{2}$∠HAG=$\frac{1}{2}$(∠HAO+∠OAG)=$\frac{1}{2}$(α+45°)=$\frac{1}{2}$α+22.5°;
(3)如圖2,∵∠EFH的平分線和∠FOC的平分線交于點N,
∴∠NFO=$\frac{1}{2}$∠EFO,∠NOF=$\frac{1}{2}$∠COF,
∴△FON中,∠N=180°-(∠NFO+∠NOF)
=180°-$\frac{1}{2}$(∠EFO+∠COF)
=180°-$\frac{1}{2}$(180°-∠AFO+180°-∠AOF)
=180°-$\frac{1}{2}$(360°-∠AFO-∠AOF)
=180°-$\frac{1}{2}$[360°-(180°-∠FAO)]
=180°-$\frac{1}{2}$(180°+∠FAO)
=90°-$\frac{1}{2}$∠FAO,
即∠N=90°-$\frac{1}{2}$∠FAH-$\frac{1}{2}$∠OAH
=90°-15°-$\frac{1}{2}$∠OAH
=75°-$\frac{1}{2}$∠OAH,
又∵∠M=$\frac{1}{2}$∠OAH+22.5°,
∴∠M+∠N=75°-$\frac{1}{2}$∠OAH+$\frac{1}{2}$∠OAH+22.5°=97.5°.
點評 本題屬于三角形綜合題,主要考查了等腰直角三角形的性質、三角形內角和定理、三角形的外角性質、角平分線的定義以及三角形面積的計算等知識的綜合應用,熟練掌握等腰直角三角形的性質和三角形內角和定理是解決問題的關鍵.


科目:初中數學 來源: 題型:填空題
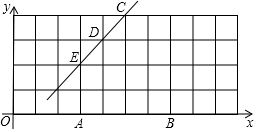 足球射門,不考慮其他因素,僅考慮射點到球門AB的張角大小時,張角越大,射門越好,己知在正方形網格中(每個正方形單位長度都為1),點A,B,C,D,E均在格點上,球員帶球沿CD方向進攻,如圖建立直角坐標系,則:
足球射門,不考慮其他因素,僅考慮射點到球門AB的張角大小時,張角越大,射門越好,己知在正方形網格中(每個正方形單位長度都為1),點A,B,C,D,E均在格點上,球員帶球沿CD方向進攻,如圖建立直角坐標系,則:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
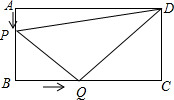 如圖所示,在長方形ABCD中,AB=6厘米,BC=12厘米,點P沿AB邊從點A開始向點B以1厘米/秒的速度移動,點Q沿BC從點B開始向點C以2厘米/秒的速度移動,如果P、Q同時出發,用t(秒)表示移動的時間(0≤t≤6).
如圖所示,在長方形ABCD中,AB=6厘米,BC=12厘米,點P沿AB邊從點A開始向點B以1厘米/秒的速度移動,點Q沿BC從點B開始向點C以2厘米/秒的速度移動,如果P、Q同時出發,用t(秒)表示移動的時間(0≤t≤6).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
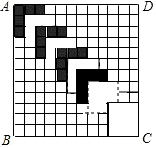 如圖,正方形ABCD的邊長為12,劃分成12×12個小正方形格.將邊長為n(n為整數,且2≤n≤11)的黑白兩色正方形紙片按圖中的方式黑白相間地擺放,第一張n×n的紙片正好蓋住正方形ABCD左上角的n×n個小正方形格,第二張紙片蓋住第一張紙片的部分恰好為(n-1)×(n-1)的正方形.如此擺放下去,最后直到紙片蓋住正方形ABCD的右下角為止.請你認真觀察思考后回答下列問題:
如圖,正方形ABCD的邊長為12,劃分成12×12個小正方形格.將邊長為n(n為整數,且2≤n≤11)的黑白兩色正方形紙片按圖中的方式黑白相間地擺放,第一張n×n的紙片正好蓋住正方形ABCD左上角的n×n個小正方形格,第二張紙片蓋住第一張紙片的部分恰好為(n-1)×(n-1)的正方形.如此擺放下去,最后直到紙片蓋住正方形ABCD的右下角為止.請你認真觀察思考后回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 工作時間t(小時) | 1 | 5 | 10 | 15 | 20 | … | t | … |
| 報酬m(元) | 20 | 100 | 200 | 300 | 400 | … | 20t | … |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC中,∠BAC=45°,過A、B兩點的⊙O交AC于點D,且OD∥BC,OD交AB于點E.
如圖,△ABC中,∠BAC=45°,過A、B兩點的⊙O交AC于點D,且OD∥BC,OD交AB于點E.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com