Question

18．閱讀材料，解答問題
數學課上，同學們興致勃勃地探討著利用不同畫圖工具畫角的平分線的方法．
小惠說：如圖1，我用相同的兩塊含30° 角的直角三角板可以畫角的平分線．畫法如下：
（1）在∠AOB 的兩邊上分別取點M，N，使OM=ON；
（2）把直角三角板按如圖所示的位置放置，兩斜邊交于點P．
射線OP是∠AOB的平分線．
小旭說：我只用刻度尺就可以畫角平分線．
請你也參與探討，解決以下問題：
（1）小惠的做法正確嗎？若正確，請給出證明，若不正確，請說明理由．
（2）請你和小旭一樣，只用刻度尺畫出圖2中∠QRS的平分線，并簡述畫圖的過程．

Answer 1

分析 （1）過O點作OC⊥PM于C，OD⊥PN于D，求出△OMC≌△OND，根據全等三角形的性質得出OC=OD，∠COM=∠DON，根據角平分線性質求出∠CPO=∠DPO．根據三角形內角和定理求出即可；
（2）根據全等三角形的判定定理SSS，用刻度尺作出即可．

解答 解：（1）小惠的做法正確．
理由如下：
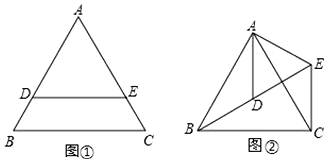
如圖1，過O點作OC⊥PM于C，OD⊥PN于D．
∴∠C=∠D=90°．
由題意，∠PMA=∠PNB=60°，
∴∠OMC=∠PMA=60°，∠OND=∠PNB=60°．
∴∠OMC=∠OND．
在△OMC和△OND中，
$\left\{\begin{array}{l}{∠CMO=∠DNO}\\{∠C=∠D}\\{OM=ON}\end{array}\right.$，
∴△OMC≌△OND（AAS），
∴OC=OD，∠COM=∠DON．
∵OC⊥PM于C，OD⊥PN于D．
∴點O在∠CPD的平分線上．
∴∠CPO=∠DPO．
∴∠COP=∠DOP．
∴∠MOP=∠NOP．
即射線OP是∠AOB的平分線．            
（2）如圖． 射線RX是∠QRS的平分線．    
簡述畫圖過程：如圖2．
用刻度尺作RV=RW，RT=RU；
連接TW，UV交于點X；
射線RX即為所求∠QRS的平分線．         

點評 本題考查了角平分線定義和全等三角形的判定和性質的應用，主要考查學生的理解能力和動手操作能力，題目比較好，難度適中．