
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 根據內心的概念證明△POC∽△QBC,根據相似三角形的性質得到$\frac{PC}{CQ}$=$\frac{OB}{OA}$,證明△PCQ∽△AOB,得到∠CPQ=∠A=15°,證明△COQ≌△MOQ即可.
解答 解:∵∠AOB=90°,∠ACO=90°,
∴∠AOC=∠ABO,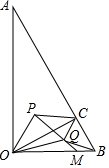 ∵P,Q分別為△AOC和△BOC的內心,
∵P,Q分別為△AOC和△BOC的內心,
∴∠POC=∠QBC,∠PCO=∠BCQ=45°,
∴△POC∽△QBC,
∴$\frac{PC}{CQ}$=$\frac{OC}{BC}$,
∵$\frac{OB}{OA}$=$\frac{OC}{BC}$,
∴$\frac{PC}{CQ}$=$\frac{OB}{OA}$,又∠AOB=∠PCQ=90°,
∴△PCQ∽△AOB,
∴∠CPQ=∠A=15°,
由內心的概念可知,∠OPC=90°+$\frac{1}{2}$×15°,
∴∠OPM=90°+$\frac{1}{2}$×15°-15°,
∵∠POM=90°-$\frac{1}{2}$∠AOC=90°-$\frac{1}{2}$×75°,
∴∠PMO=45°,
在△COQ和△MOQ中,
$\left\{\begin{array}{l}{∠COQ=∠MOQ}\\{∠OCQ=∠OMQ}\\{OQ=OQ}\end{array}\right.$,
∴△COQ≌△MOQ,
∴OM=OC=1,
故選:B.
點評 本題考查的是三角形的內接圓和內心的概念、相似三角形的判定和性質、全等三角形的判定和性質,掌握三角形的內接圓和內心的概念是解題的關鍵.


科目:初中數學 來源: 題型:填空題
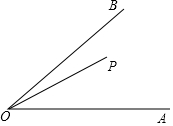 如圖,∠AOB=45°,P是∠AOB內一點,PO=10,Q、R分別是OA、OB上的動點,則△PQR周長的最小值為10$\sqrt{2}$.
如圖,∠AOB=45°,P是∠AOB內一點,PO=10,Q、R分別是OA、OB上的動點,則△PQR周長的最小值為10$\sqrt{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
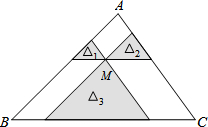 如圖,點M是△ABC內一點,過點M分別作直線平行于△ABC的各邊,所形成的三個小三角形△1,△2,△3(圖中的陰影部分)的面積是4,9,49,則△ABC的面積是( )
如圖,點M是△ABC內一點,過點M分別作直線平行于△ABC的各邊,所形成的三個小三角形△1,△2,△3(圖中的陰影部分)的面積是4,9,49,則△ABC的面積是( )| A. | 62 | B. | 186 | C. | 132 | D. | 144 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 油桶制造廠的某車間主要負責生產制造油桶用的圓形鐵片和長方形鐵片,該車間有工人42人,每個工人平均每小時可以生產圓形鐵片102片或者長方形鐵片80片,如圖,一個油桶由兩個圓形鐵片和一個長方形鐵片相配套,生產圓形鐵片和長方形鐵片的工人各為多少人時,才能使生產的鐵片恰好配套?
油桶制造廠的某車間主要負責生產制造油桶用的圓形鐵片和長方形鐵片,該車間有工人42人,每個工人平均每小時可以生產圓形鐵片102片或者長方形鐵片80片,如圖,一個油桶由兩個圓形鐵片和一個長方形鐵片相配套,生產圓形鐵片和長方形鐵片的工人各為多少人時,才能使生產的鐵片恰好配套?查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 16 | B. | 20 | C. | 32 | D. | 40 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com