
 如圖,AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.點P在射線AB上以1cm/s的速度由點A出發沿射線AB方向運動,同時,點Q在射線DB上由點D出發沿射線DB方向運動.它們運動的時間為t(s).
如圖,AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.點P在射線AB上以1cm/s的速度由點A出發沿射線AB方向運動,同時,點Q在射線DB上由點D出發沿射線DB方向運動.它們運動的時間為t(s).分析 (1)根據Q和P的運動速度結合時間可得AP=1cm,DQ=2cm,進而可得BP=3,BQ=1,然后利用SAS判定△CAP≌△PBQ,根據全等三角形的性質可得∠APC=∠BQA,然后再根據直角三角形的性質可推出∠APC+∠QPB=90°,進而可得CP⊥PQ;
(2)此題要分3種情況分別討論,①若點P在AB上,點Q在BN上,②若點P在BM上,點Q在BN上.
解答 (1)VQ=2VP=2m/s,
∵t=1s,
∴AP=1cm,DQ=2cm,
∴BP=AB-AP=3cm,BQ=BD-DQ=1cm,
在△CAP和△PBQ中$\left\{\begin{array}{l}{AC=BP}\\{∠A=∠PBQ=90°}\\{AP=BQ}\end{array}\right.$,
∴△CAP≌△PBQ(SAS),
∴∠APC=∠BQA,
∵∠BQP+∠QPB=90°,
∴∠APC+∠QPB=90°,
∴∠CPQ=180°-90°=90°,
∴CP⊥PQ;
(2)若點P在AB上,點Q在BN上,
且△APC≌△BPQ,
如圖 1,t=2,x=3,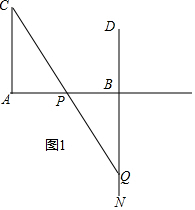
若點P在AB上,點Q在BN上,
且△APC≌△BQP;
如圖2:t=1,x=4,△APC≌△BQP;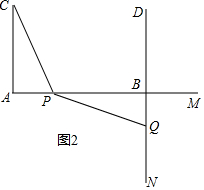
如圖3,若點P在BM上,點Q在BN上,t=7,x=$\frac{10}{7}$,△APC≌△BQP;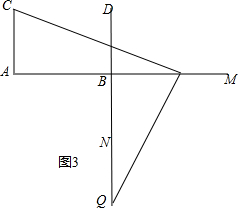 .
.
點評 此題主要考查了全等三角形的判定,關鍵是掌握全等三角形的判定方法:SSS、SAS、ASA、AAS、HL.


科目:初中數學 來源: 題型:解答題
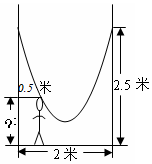 如圖,小明的父親在相距2米的兩棵樹間拴了一根繩子,給小明做了一個簡易的秋千.拴繩子的地方距地面高都是2.5米,繩子自然下垂呈拋物線狀,身高1米的小明距較近的那棵樹0.5米時,頭部剛好接觸到繩子,則繩子的最低點距地面的距離為多少米?
如圖,小明的父親在相距2米的兩棵樹間拴了一根繩子,給小明做了一個簡易的秋千.拴繩子的地方距地面高都是2.5米,繩子自然下垂呈拋物線狀,身高1米的小明距較近的那棵樹0.5米時,頭部剛好接觸到繩子,則繩子的最低點距地面的距離為多少米?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com