
 在平面直角坐標系中,$A(6\sqrt{3},0),B(0,6)$,動點M從點O開始沿OA以$\sqrt{3}$cm/s的速度向點A移動,動點N從點A開始沿AB以2cm/s的速度向點B移動.如果M,N分別從O,A同時移動,移動時間為t(0<t<6).
在平面直角坐標系中,$A(6\sqrt{3},0),B(0,6)$,動點M從點O開始沿OA以$\sqrt{3}$cm/s的速度向點A移動,動點N從點A開始沿AB以2cm/s的速度向點B移動.如果M,N分別從O,A同時移動,移動時間為t(0<t<6).分析 (1)在Rt△AOB中,求出tan∠OAB的值,即可解決問題.
(2)設直線AB的表達式為y=kx+b,把$A(6\sqrt{3},0),B(0,6)$代入轉化為解方程組解決問題.
(3)存在.分三種情形:①當AM=AN時,②當NA=MN時,③當MA=MN時,分別列出方程解決問題.
解答 解:(1)∵$A(6\sqrt{3},0),B(0,6)$,
∴OA=6$\sqrt{3}$,OB=6,
∴tan∠OAB=$\frac{OB}{OA}$=$\frac{6}{6\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠OAB=30°,
故答案為30.
(2)設直線AB的表達式為y=kx+b,
把$A(6\sqrt{3},0),B(0,6)$代入上式得$\left\{\begin{array}{l}{b=6}\\{6\sqrt{3}k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=6}\end{array}\right.$,
∴直線AB的解析式為y=-$\frac{\sqrt{3}}{3}$x+6.
(3)存在.分三種情形:
①當AM=AN時,6$\sqrt{3}$-$\sqrt{3}$t=2t,
解得t=12$\sqrt{3}$-18,
②當NA=MN時,$\sqrt{3}$t=$\frac{6\sqrt{3}-\sqrt{3}t}{2}$,
解得t=2,
③當MA=MN時,$\frac{6\sqrt{3}-\sqrt{3}t}{2}$•$\sqrt{3}$=t,
解得t=3.6,
綜上所述,當t=12$\sqrt{3}$-18或2或3.6s時,△AMN是等腰三角形.
點評 本題考查三角形綜合題、銳角三角函數(shù)、等腰三角形的判定和性質,一元一次方程等知識,解題的關鍵是靈活運用所學知識,學會用分類討論的思想思考問題,把問題轉化為方程解決,屬于中考常考題型.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:初中數(shù)學 來源: 題型:填空題
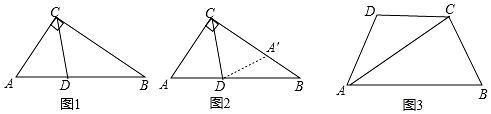
 如圖,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一點C,延長AA1到A2,使得A1A2=A1C,在A2C上取一點D,延長A1A2到A3,使得A2A3=A2D,按此做法進行下去,∠EA3A2的度數(shù)為20°,∠A的度數(shù)為80°.
如圖,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一點C,延長AA1到A2,使得A1A2=A1C,在A2C上取一點D,延長A1A2到A3,使得A2A3=A2D,按此做法進行下去,∠EA3A2的度數(shù)為20°,∠A的度數(shù)為80°.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
| 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
| 路程(km) | -8 | -11 | -14 | 0 | -16 | +41 | +8 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
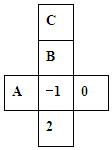 如圖是一個正方體紙盒的表面展開圖,若在其中三個正方形A、B、C內分別填入適當?shù)臄?shù),使它折成正方體后相對的面上的兩數(shù)互為相反數(shù),則填在正方形A、B、C內的三個數(shù)依次為( )
如圖是一個正方體紙盒的表面展開圖,若在其中三個正方形A、B、C內分別填入適當?shù)臄?shù),使它折成正方體后相對的面上的兩數(shù)互為相反數(shù),則填在正方形A、B、C內的三個數(shù)依次為( )| A. | -2,1,0 | B. | 1,-2,0 | C. | 0,-2,1 | D. | -2,0,1 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com