
 在一次課外實踐活動中,同學們要測量某公園人工湖兩側A、B兩個涼亭之間的距離.現測得AC=300m,BC=700m,∠CAB=120°,請計算A、B兩個涼亭之間的距離.
在一次課外實踐活動中,同學們要測量某公園人工湖兩側A、B兩個涼亭之間的距離.現測得AC=300m,BC=700m,∠CAB=120°,請計算A、B兩個涼亭之間的距離. 分析 作CD⊥AB交BA的延長線于點D.根據鄰補角的定義,求出∠ACD的度數,在Rt△ACD中,利用∠CAD的正弦、余弦求AD、CD,在Rt△BCD中利用勾股定理求出BD.根據線段的和差關系求出AB.
解答 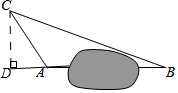 解:過點C作CD⊥BA,交BA的延長線于點D.
解:過點C作CD⊥BA,交BA的延長線于點D.
∵∠CAB=120°,∴∠CAD=60°.
在Rt△ACD中,∵sin60°=$\frac{CD}{AC}$,cos60°=$\frac{AD}{AC}$,
∴CD=sin60°×AC=$\frac{\sqrt{3}}{2}$×300=150$\sqrt{3}$(m),
AD=cos60°×AC=$\frac{1}{2}$×300=150(m)
在Rt△BCD中,BD=$\sqrt{B{C}^{2}-C{D}^{2}}$
=$\sqrt{70{0}^{2}-(150\sqrt{3)^{2}}}$=650(m)
∴AB=BD-AD=650-150=500(m)
答:A、B兩個涼亭之間的距離為500m.
點評 本題考查了三角函數及勾股定理.解決本題的關鍵是過點C作CD⊥AB構造直角三角形.


科目:初中數學 來源: 題型:選擇題
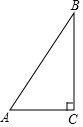 如圖,在Rt△ABC中,∠C=90°,AC=9,BC=12,則點C到AB的距離是( )
如圖,在Rt△ABC中,∠C=90°,AC=9,BC=12,則點C到AB的距離是( )| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{3\sqrt{3}}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知AB為⊙O的直徑,點E在⊙O上,∠EAB的平分線交⊙O于點C,過點C作AE的垂線,垂足為D,直線DC與AB的延長線交于點P.
如圖,已知AB為⊙O的直徑,點E在⊙O上,∠EAB的平分線交⊙O于點C,過點C作AE的垂線,垂足為D,直線DC與AB的延長線交于點P.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
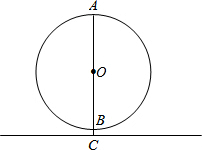 如圖,⊙O是夢幻谷的摩天輪示意圖,⊙O的最高處A到地面的距離是23米,最低處B到地面的距離是3米,AB是直徑,摩天輪勻速轉動,從B處乘坐繞摩天輪一周要6分鐘,
如圖,⊙O是夢幻谷的摩天輪示意圖,⊙O的最高處A到地面的距離是23米,最低處B到地面的距離是3米,AB是直徑,摩天輪勻速轉動,從B處乘坐繞摩天輪一周要6分鐘,查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖所示,兩個等腰三角形的頂角互補,其中一個三角形的邊長是a,a,b(a>b),另一個三角形的邊長為b,b,a,則這兩個三角形的六個內角中,度數最大的是( )
如圖所示,兩個等腰三角形的頂角互補,其中一個三角形的邊長是a,a,b(a>b),另一個三角形的邊長為b,b,a,則這兩個三角形的六個內角中,度數最大的是( )| A. | 75° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 5個 | B. | 4個 | C. | 3個 | D. | 2個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com