
 如圖,AC=BC,點0為AB的中點,AC⊥BC,∠MON=45°,求證:CN+MN=AM.
如圖,AC=BC,點0為AB的中點,AC⊥BC,∠MON=45°,求證:CN+MN=AM. 分析 連接CO,在線段AM上截取AQ=CN,連接OQ,由O為CA、CB的垂直平分線的交點,根據線段垂直平分線的性質得到OA=OB=OC,又AC=BC得到∠A=∠B=45°,再根據三線合一的性質得到CO與AB垂直且CO為頂角的平分線,由∠A和∠B求出∠ACB為直角,得到∠OCB也為45°,由SAS得到△AOQ與△CON全等,由全等三角形的性質得出OQ=ON,∠AOQ=∠CON,等量代換得到∠QON為直角,又∠MON為45°,所以∠QOM也為45°,得兩角相等,然后由OQ=ON,求出的兩角相等,OM為公共邊,利用SAS得到△OQM與△MON全等,根據全等三角形的對應邊相等得到QM=MN,由AM=AQ+QM,等量代換即可得證;
解答 證明:連接OC,在AM上截取AQ=CN,連接OQ,如圖所示: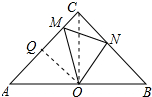
∵AC=BC,點O為AB的中點,AC⊥BC,
∴OC=OA=OB,
∵AC=BC,∴OC⊥AB,CO平分∠ACB,
∴∠A=∠B=45°,即∠ACB=90°,
∴∠OCN=45°,即∠OCN=∠A=45°,
在△AOQ和△CON中,$\left\{\begin{array}{l}{AQ=CN}&{\;}\\{∠A=∠OCN}&{\;}\\{AO=OC}&{\;}\end{array}\right.$,
∴△AOQ≌△CON(SAS),
∴OQ=ON,∠AOQ=∠CON,
∵OC⊥AB,
∴∠AOC=∠AOQ+∠COQ=90°,
∴∠CON+∠COQ=90°,
即∠QON=90°,
又∠MON=45°,
∴∠QOM=45°,
在△QOM和△NOM中,$\left\{\begin{array}{l}{OQ=ON}&{\;}\\{∠MON=∠QOM}&{\;}\\{OM=OM}&{\;}\end{array}\right.$,
∴△QOM≌△NOM(SAS),
∴QM=NM,
∴CN+MN=AQ+QM=AM.
點評 此題考查了全等三角形的判定與性質、等腰直角三角形的性質;線段的和、差、倍、分問題通常情況下先在較長的線段上截取一段與其中一條線段相等,然后構造全等三角形證明剩下的線段與另一條線段相等,本題的突破點是截取出AQ=CN,構造全等三角形,證明QM=NM.


科目:初中數學 來源: 題型:選擇題
| A. | V=30P | B. | P=V+900 | C. | P=30V | D. | PV=30 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
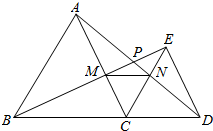 已知如圖:△ABC和△DEC都是等邊三角形,D是BC延長線上一點,AD與BE相交于點P,AC、BE相交于點M,AD、CE相交于點N,則下列五個結論:①AD=BE;②AN=BM;③∠APM=60°;④△CMN是等邊三角形;⑤MN∥BD;⑥PC平分∠BPD,其中,正確的是①②③④⑤⑥(填寫序號)
已知如圖:△ABC和△DEC都是等邊三角形,D是BC延長線上一點,AD與BE相交于點P,AC、BE相交于點M,AD、CE相交于點N,則下列五個結論:①AD=BE;②AN=BM;③∠APM=60°;④△CMN是等邊三角形;⑤MN∥BD;⑥PC平分∠BPD,其中,正確的是①②③④⑤⑥(填寫序號)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
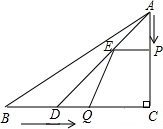 如圖,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,點D在BC上,且CD=3cm,現有兩個動點P,Q分別從點A和點B同時出發,其中點P以1厘米/秒的速度沿AC向終點C運動;點Q以1.25厘米/秒的速度沿BC向終點C運動.過點P作PE∥BC交AD于點E,連接EQ.設動點運動時間為t秒(t>0).當一個點到達終點時,另一個點隨之停止運動.
如圖,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,點D在BC上,且CD=3cm,現有兩個動點P,Q分別從點A和點B同時出發,其中點P以1厘米/秒的速度沿AC向終點C運動;點Q以1.25厘米/秒的速度沿BC向終點C運動.過點P作PE∥BC交AD于點E,連接EQ.設動點運動時間為t秒(t>0).當一個點到達終點時,另一個點隨之停止運動.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com