
| A. | 周長相等的兩個三角形全等 | |
| B. | 等底等高的兩個三角形全等 | |
| C. | 有兩邊和一角對應(yīng)相等的兩個三角形全等 | |
| D. | 有一條直角邊和斜邊上的高對應(yīng)相等的兩個直角三角形全等 |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
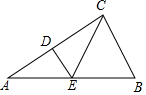 在△ABC中,DE垂直平分AC交AB于點E,∠A=30°,∠BCE=50°,則∠B=( )
在△ABC中,DE垂直平分AC交AB于點E,∠A=30°,∠BCE=50°,則∠B=( )| A. | 60° | B. | 70° | C. | 80° | D. | 50° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
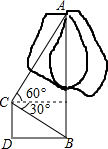 為改變哈爾濱市的交通狀況,在大直街拓寬工程中,要伐掉一棵樹AB,在地面上事先劃定以B為圓心,半徑與AB等長的圓形危險區(qū),現(xiàn)在某工人站在離B點3米遠的D處,從C點測得樹的頂端A點的仰角為60°,樹的底部B點的俯角為30°,那么距離B點7米遠,才是安全區(qū)域.(結(jié)果保留整數(shù),$\sqrt{3}$≈1.732)
為改變哈爾濱市的交通狀況,在大直街拓寬工程中,要伐掉一棵樹AB,在地面上事先劃定以B為圓心,半徑與AB等長的圓形危險區(qū),現(xiàn)在某工人站在離B點3米遠的D處,從C點測得樹的頂端A點的仰角為60°,樹的底部B點的俯角為30°,那么距離B點7米遠,才是安全區(qū)域.(結(jié)果保留整數(shù),$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,已知一次函數(shù)y=k1x+b的圖象分別與x軸、y軸的正半軸交于A,B兩點,且與反比例函數(shù)y=$\frac{{k}_{2}}{x}$交于C,E兩點,點C在第二象限,過點C作CD⊥x軸于點D,OA=OB=4,OD=2.
如圖,已知一次函數(shù)y=k1x+b的圖象分別與x軸、y軸的正半軸交于A,B兩點,且與反比例函數(shù)y=$\frac{{k}_{2}}{x}$交于C,E兩點,點C在第二象限,過點C作CD⊥x軸于點D,OA=OB=4,OD=2.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
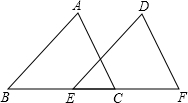 如圖,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一個條件后,仍然不能證明△ABC≌△DEF,這個條件是( )
如圖,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一個條件后,仍然不能證明△ABC≌△DEF,這個條件是( )| A. | ∠A=∠D | B. | BE=FC | C. | ∠ACB=∠F | D. | AC=DF |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com