
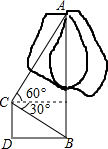
 為改變哈爾濱市的交通狀況,在大直街拓寬工程中,要伐掉一棵樹AB,在地面上事先劃定以B為圓心,半徑與AB等長的圓形危險區,現在某工人站在離B點3米遠的D處,從C點測得樹的頂端A點的仰角為60°,樹的底部B點的俯角為30°,那么距離B點7米遠,才是安全區域.(結果保留整數,$\sqrt{3}$≈1.732)
為改變哈爾濱市的交通狀況,在大直街拓寬工程中,要伐掉一棵樹AB,在地面上事先劃定以B為圓心,半徑與AB等長的圓形危險區,現在某工人站在離B點3米遠的D處,從C點測得樹的頂端A點的仰角為60°,樹的底部B點的俯角為30°,那么距離B點7米遠,才是安全區域.(結果保留整數,$\sqrt{3}$≈1.732) 分析 根據題意可知所求的問題實際上就是求AB得長,由題目中的數據和銳角三角函數可以求得AB的長,從而本題得以解決.
解答  解:由題意可得,如右圖所示,
解:由題意可得,如右圖所示,
BD=3米,∠CDB=90°,
∵CE∥DB,∠ECB=30°,
∴∠ECB=∠CBD=30°,
∴CD=BD•tan∠CBD=3×tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}米$,
∵CE=BD=3米,∠CEA=90°,∠ACE=60°,
∴AE=CE•tan60°=3×$\sqrt{3}$=3$\sqrt{3}$米,
∴AB=AE+EB=$\sqrt{3}+3\sqrt{3}$=4$\sqrt{3}$≈4×1.732=6.928≈7米,
故答案為:7.
點評 本題考查解直角三角形的應用-仰角俯角問題,解答此類問題的關鍵是明確題意,利用銳角三角函數解答,注意最后結果要保留整數.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
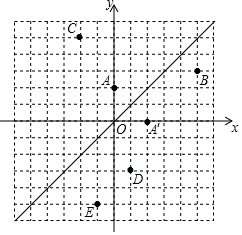 如圖,在平面直角坐標系中,直線l是第一、三象限的角平分線.
如圖,在平面直角坐標系中,直線l是第一、三象限的角平分線.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 周長相等的兩個三角形全等 | |
| B. | 等底等高的兩個三角形全等 | |
| C. | 有兩邊和一角對應相等的兩個三角形全等 | |
| D. | 有一條直角邊和斜邊上的高對應相等的兩個直角三角形全等 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在△ABC中,D為AB邊上一點,DE∥BC交AC于點E,若$\frac{AD}{BD}=\frac{3}{4}$,DE=4,則BC的長為$\frac{28}{3}$.
如圖,在△ABC中,D為AB邊上一點,DE∥BC交AC于點E,若$\frac{AD}{BD}=\frac{3}{4}$,DE=4,則BC的長為$\frac{28}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
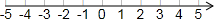 已知在紙面上有一數軸(如圖),折疊紙面.
已知在紙面上有一數軸(如圖),折疊紙面.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y>1 | B. | 0<y<1 | C. | y>2 | D. | 0<y<2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com