
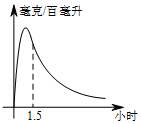
 實驗數據顯示:一般成人喝半斤低度白酒后,1.5小時內(包括1.5小時)其血液中酒精含量y(毫克/百毫升)與時間x(時)的關系可近似地用二次函數y=-200x2+400x表示,1.5小時后(包括1.5小時)y與x可近似地用反比例函數y=$\frac{k}{x}$(k>0)表示(如圖所示)
實驗數據顯示:一般成人喝半斤低度白酒后,1.5小時內(包括1.5小時)其血液中酒精含量y(毫克/百毫升)與時間x(時)的關系可近似地用二次函數y=-200x2+400x表示,1.5小時后(包括1.5小時)y與x可近似地用反比例函數y=$\frac{k}{x}$(k>0)表示(如圖所示)分析 (1)利用y=-200x2+400x=-200(x-1)2+200確定最大值;
(2)①先求出反比例函數解析式,再分別求得y≥80時x的范圍,即可知醉酒持續的時間;②計算出反比例函數中y<20時x的范圍,就可得酒精含量低于20所需時間.
解答 解:(1)y=-200x2+400x=-200(x-1)2+200,
∴x=1時血液中的酒精含量達到最大值,最大值為200(毫克/百毫升);
(2)①當x=1.5時,y=-200x2+400x=-200×2.25+400×1.5=150,
∴k=1.5×150=225,
即x>1.5時,y=$\frac{225}{x}$;
當0<x≤1.5時,由-200(x-1)2+200≥80,
解得:5-$\sqrt{15}$≤x≤5+$\sqrt{15}$,
當x>1.5時,由$\frac{225}{x}$≥80得x≤$\frac{45}{16}$,
則當5-$\sqrt{15}$≤x≤$\frac{45}{16}$時,其酒精含量屬于“醉酒駕車”范圍;
$\frac{45}{16}$-5+$\sqrt{15}$≈1.8,
答:有1.8小時其酒精含量屬于“醉酒駕車”范圍;
②由$\frac{225}{x}$<20可得x>11.25,
即從飲酒后11.25小時才能駕車去上班,
則第二天早上7:15才能駕車去上班.
點評 此題主要考查了二次函數和反比例函數綜合應用,根據圖象得出正確信息是解題關鍵,能夠從實際問題中抽象出二次函數模型是解答的重點.


 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:初中數學 來源: 題型:解答題
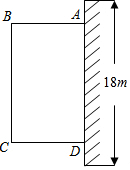 為了改善小區環境,某小區決定要在一塊一邊靠墻(墻長18m)的空地上修建一個矩形綠化帶ABCD,綠化帶一邊靠墻,另三邊用總長為40m的柵欄圍住(如圖),設綠化帶BC邊長為xm,綠化帶的面積為ym2.
為了改善小區環境,某小區決定要在一塊一邊靠墻(墻長18m)的空地上修建一個矩形綠化帶ABCD,綠化帶一邊靠墻,另三邊用總長為40m的柵欄圍住(如圖),設綠化帶BC邊長為xm,綠化帶的面積為ym2.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
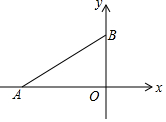 如圖,在平面直角坐標系中,A,B兩點的坐標分別為(-4,0),(0,3),連接AB.點P在第二象限,若以點P,A,B為頂點的三角形是等腰直角三角形,則點P坐標為(-$\frac{7}{2}$,$\frac{7}{2}$)或(-3,7)或(-7,4).
如圖,在平面直角坐標系中,A,B兩點的坐標分別為(-4,0),(0,3),連接AB.點P在第二象限,若以點P,A,B為頂點的三角形是等腰直角三角形,則點P坐標為(-$\frac{7}{2}$,$\frac{7}{2}$)或(-3,7)或(-7,4).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com