
分析 (1)根據題意可以得到yA、yB與x之間的函數關系式;
(2)根據(1)中函數關系式,利用分類討論的數學方法可以解答本題.
解答 解:(1)由題意可得,
yA=(20×60+20x×2)×0.9=36x+1080,
當2≤x≤4時,yB=20×60=1200,
當x>4時,yB=20×60+(x-4)×20×2=40x+1040,
即yA與x之間的函數關系式為yA=36x+1080,
yB與x之間的函數關系式為yB=$\left\{\begin{array}{l}{1200}&{(2≤x≤4)}\\{40x+1040}&{(x>4)}\end{array}\right.$;
(2)由題意可得,
當36x+1080<1200時,x<$\frac{10}{3}$,
∴當x為2或3時,從A商店購買,當x為4時,在B商店購買,
當36x+1080<40x+1040時,得x>10,
∴當4<x<10時,在B商店購買,
當x=10時,在哪家商店購買都可以,
當x>10時,在A商店購買,
由上可得,當x=2,x=3或x>10(x取整數)時,在A商店購買,
當x=10時,在哪家商店購買都可以,
當4≤x<10(x取整數)時,在B商店購買.
點評 本題考查一次函數的應用,解答本題的關鍵是明確題意,找出所求問題需要的條件,利用分類討論的數學思想解答,注意題目中x≥2.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源: 題型:解答題
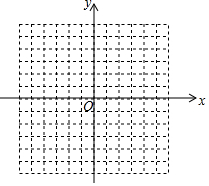 如圖,方格紙中每個小正方形的邊長都是單位1,△ABC的三個頂點都在格點(即這些小正方形的頂點)上,且它們的坐標分別是A(2,-3),B(5,-1),C(-1,3),結合所給的平面直角坐標系,解答下列問題:
如圖,方格紙中每個小正方形的邊長都是單位1,△ABC的三個頂點都在格點(即這些小正方形的頂點)上,且它們的坐標分別是A(2,-3),B(5,-1),C(-1,3),結合所給的平面直角坐標系,解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
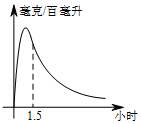 實驗數據顯示:一般成人喝半斤低度白酒后,1.5小時內(包括1.5小時)其血液中酒精含量y(毫克/百毫升)與時間x(時)的關系可近似地用二次函數y=-200x2+400x表示,1.5小時后(包括1.5小時)y與x可近似地用反比例函數y=$\frac{k}{x}$(k>0)表示(如圖所示)
實驗數據顯示:一般成人喝半斤低度白酒后,1.5小時內(包括1.5小時)其血液中酒精含量y(毫克/百毫升)與時間x(時)的關系可近似地用二次函數y=-200x2+400x表示,1.5小時后(包括1.5小時)y與x可近似地用反比例函數y=$\frac{k}{x}$(k>0)表示(如圖所示)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
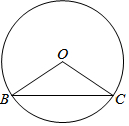 在⊙O中,己知弦BC所對的圓周角∠BAC與圓心角∠BOC互補.
在⊙O中,己知弦BC所對的圓周角∠BAC與圓心角∠BOC互補.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 19 | B. | 20 | C. | 21 | D. | 22 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com