
分析 (1)根據拋物線的對稱軸x=1,AB=4,推出A(-1,0),B(3,0),推出頂點C坐標(1,-2),設拋物線的解析式為y=a(x-1)2-2,把(-1,0)代入得a=$\frac{1}{2}$,由此即可解決問題.
(2)如圖1中,作DN⊥x軸于N,作FM⊥x軸于M,連接AF.只要證明△DEN≌△EFM,推出DN=EM,EN=FM,因為A(-1,0),C(1,-2),所以tan∠CAO=$\frac{2}{2}$=1,推出∠DAN=∠OAC=45°,推出DN=AN=EM,推出EN=AM=FM,推出∠FAM=45°,推出直線AF的解析式為y=x+1,由$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\end{array}\right.$解方程組即可確定點F坐標.
(3)如圖2中,作DN⊥x軸于N,FM⊥x軸于M,DJ⊥EG于J,延長EG使得EJ=JK,在EK的延長線上截取KP=DJ,作PQ⊥PE,截取PQ=KJ,連接DQ交拋物線于H.
只要證明∠HDF=2∠DEA,求得直線DQ的解析式為y=3x+15,解方程組:$\left\{\begin{array}{l}{y=3x+15}\\{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\end{array}\right.$即可解決問題.
解答 解:(1)對于拋物線y=ax2-2ax+b,對稱軸x=-$\frac{-2a}{2a}$=1,
∵AB=4,
∴A(-1,0),B(3,0),頂點C坐標(1,-2),
設拋物線的解析式為y=a(x-1)2-2,把(-1,0)代入得a=$\frac{1}{2}$,
∴拋物線是解析式為y=$\frac{1}{2}$(x-1)2-2,即y=$\frac{1}{2}$x2-x-$\frac{3}{2}$,
∴a=$\frac{1}{2}$,b=-$\frac{3}{2}$.
(2)如圖1中,作DN⊥x軸于N,作FM⊥x軸于M,連接AF.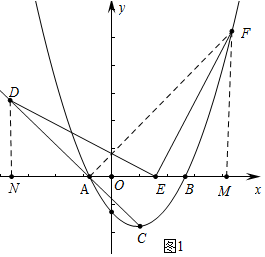
∵∠DNE=∠EMF=∠DEF=90°,
∴∠DEN+∠FEM=90°,∠FEM+∠EFM=90°,
∴∠DEN=∠EFM,
在△DEN和△EFM中,
$\left\{\begin{array}{l}{∠DEN=∠EFM}\\{∠DNE=∠EMF}\\{DE=EF}\end{array}\right.$,
∴△DEN≌△EFM,
∴DN=EM,EN=FM,
∵A(-1,0),C(1,-2),
∴tan∠CAO=$\frac{2}{2}$=1,
∴∠DAN=∠OAC=45°,
∴DN=AN=EM,
∴EN=AM=FM,
∴∠FAM=45°,
∴直線AF的解析式為y=x+1,
由$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=5}\\{y=6}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$,
∴點F的坐標為(5,6).
(3)如圖2中,作DN⊥x軸于N,FM⊥x軸于M,DJ⊥EG于J,延長EG使得EJ=JK,在EK的延長線上截取KP=DJ,作PQ⊥PE,截取PQ=KJ,連接DQ交拋物線于H.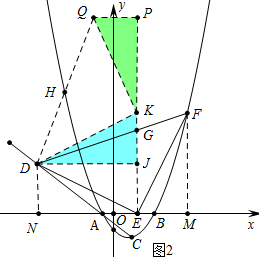
∵DN∥EG∥FM,DG=2FG,
∴$\frac{EN}{EM}$=$\frac{DG}{GF}$=2,
∴FM=EN=2EM,
∵FM=6,
∴DN=EM=EJ=KJ=3,DJ=EN=6,
∵DJ=PK=6,PQ=KJ=3,∠DJK=∠QPK,
∴△DJK≌△KPQ,
∴DK=KQ,∠KDJ=∠QKP,
∵∠KDJ+∠DKJ=90°,
∴∠DKJ+∠QKP=90°,
∴∠DKQ=90°,
∴∠KDQ=∠DQK=45°,
∵DK=DE,DJ⊥EK,
∠JDK=∠JDE=∠DEA,
∴∠KDE=2∠DEA=∠EDF+∠KDF=45°+∠KDF=∠QDK+∠KDG=∠QDF,
∴∠HDF=2∠DEA,
∵Q(-1,12),D(-4,3),
∴直線DQ的解析式為y=3x+15,
由$\left\{\begin{array}{l}{y=3x+15}\\{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-3}\\{y=6}\end{array}\right.$或$\left\{\begin{array}{l}{x=11}\\{y=48}\end{array}\right.$,
∵點H在第二象限,
∴點H的坐標為(-3,6).
點評 本題考查二次函數綜合題、一次函數的應用、全等三角形的判定和性質、等腰直角三角形的性質、銳角三角函數等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形解決問題,學會構建一次函數,利用方程組求兩個函數的交點坐標,本題體現了數形結合的思想,屬于中考壓軸題.


科目:初中數學 來源: 題型:解答題
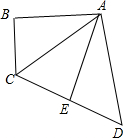 如圖,在四邊形ABCD中,∠B=90°,點E是CD的中點,連結AE,AC,且AC=AD,AB=AE.
如圖,在四邊形ABCD中,∠B=90°,點E是CD的中點,連結AE,AC,且AC=AD,AB=AE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
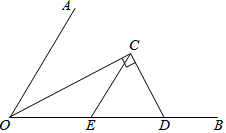 如圖,∠AOB=60°,OC平分∠AOB,C為角平分線上一點,過點C作CD⊥OC,垂足為C,交OB于點D,CE∥OA交OB于點E.
如圖,∠AOB=60°,OC平分∠AOB,C為角平分線上一點,過點C作CD⊥OC,垂足為C,交OB于點D,CE∥OA交OB于點E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知直線l與⊙O相離,OA⊥l于點A,OA=5,OA與⊙O相交于點P,AB與⊙O相切于點B,BP的延長線交直線l于點C.
如圖,已知直線l與⊙O相離,OA⊥l于點A,OA=5,OA與⊙O相交于點P,AB與⊙O相切于點B,BP的延長線交直線l于點C.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1.$\stackrel{•}{3}$$\stackrel{•}{4}$ | B. | $\frac{22}{7}$ | C. | $\sqrt{16}$ | D. | 0.020020002… |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,AB 為⊙O 的切線,切點為 B,連接 AO 與⊙O 交與點 C,BD 為⊙O 的直徑,連接 CD,若∠A=30°,OA=2,則圖中陰影部分的面積為( )
如圖,AB 為⊙O 的切線,切點為 B,連接 AO 與⊙O 交與點 C,BD 為⊙O 的直徑,連接 CD,若∠A=30°,OA=2,則圖中陰影部分的面積為( )| A. | $\frac{π}{3}-\frac{{\sqrt{3}}}{4}$ | B. | $\frac{4π}{3}-2\sqrt{3}$ | C. | $π-\sqrt{3}$ | D. | $\frac{4}{3}π-\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (1)在如圖所示的方格紙中,經過線段AB外一點C,畫線段AB的垂線CH(垂足為H)和平行線EF.(畫出的線請用鉛筆描粗描黑)
(1)在如圖所示的方格紙中,經過線段AB外一點C,畫線段AB的垂線CH(垂足為H)和平行線EF.(畫出的線請用鉛筆描粗描黑)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com