Question

11．如圖，已知直線l與⊙O相離，OA⊥l于點A，OA=5，OA與⊙O相交于點P，AB與⊙O相切于點B，BP的延長線交直線l于點C．
（1）若CP=2$\sqrt{5}$，求⊙O的半徑；
（2）若在⊙O上存在點Q，使△AQC是以AC為底邊的等腰三角形，求⊙O的半徑r的取值范圍．

Answer 1

分析 （1）連接OB，延長AP交⊙O于D，連接BD，求出∠OBP+∠ABP=90°，∠ACP+∠CPB=90°，∠OBP=∠OPB，推出∠ACP=∠ABC，可求得AB=AC，設圓半徑為r，根據勾股定理得出AB²=OA²-OB²=5²-r²，AC²=PC²-PA²=（2$\sqrt{5}$）²-（5-r）²，根據AC=AB得出方程5²-r²=（2$\sqrt{5}$）²-（5-r）²，可求得半徑；
（2）根據已知得出Q在AC的垂直平分線上，作出線段AC的垂直平分線MN，作OE⊥MN，求出OE＜r，即可求出r范圍．

解答 解：
（1）如圖1，連接OB，延長AP交⊙O于D，連接BD，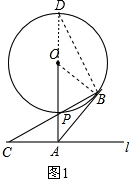

∵AB切⊙O于B，OA⊥AC，
∴∠OBA=∠OAC=90°，
∴∠OBP+∠ABP=90°，∠ACP+∠CPA=90°，
∵OP=OB，
∴∠OBP=∠OPB．
∵∠OPB=∠APC，
∴∠ACP=∠ABC，
∴AB=AC．
設圓半徑為r，則由OA=5得，OP=OB=r，PA=5-r．
又∵PC=2$\sqrt{5}$，
∴AB²=OA²-OB²=5²-r²，AC²=PC²-PA²=（2$\sqrt{5}$）²-（5-r）²，
∵由（1）知AC=AB，
∴5²-r²=（2$\sqrt{5}$）²-（5-r）²，
解得：r=3，
即⊙O的半徑是3；

（2）作出線段AC的垂直平分線MN，作OE⊥MN，如圖2，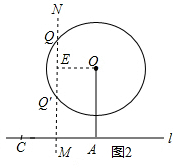

∴OE=$\frac{1}{2}$AC=$\frac{1}{2}$AB=$\frac{1}{2}$$\sqrt{{5}^{2}-{r}^{2}}$，
又∵圓O與直線MN有交點，
∴OE=$\frac{1}{2}$$\sqrt{{5}^{2}-{r}^{2}}$≤r，
∴$\sqrt{{5}^{2}-{r}^{2}}$≤2r，即25-r²≤4r²，
∴r²≥5，
∴r≥$\sqrt{5}$．
∵OA=5，直線l與⊙O相離，
∴r＜5，
∴$\sqrt{5}$≤r＜5．

點評 本題主要考查了切線的性質，等腰三角形的性質和判定，勾股定理，直線與圓的位置關系等知識點的應用，主要培養學生運用性質進行推理和計算的能力．本題綜合性比較強，有一定的難度．