Question

7．如圖，在圓內接四邊形ABCD中，∠A=52.5°，∠B=97.5°，∠AOB=120°（O為圓心），AB=a，BC=b，CD=c，DA=d，用a、b、c、d表示四邊形ABCD的面積．

Answer 1

分析 連接AC，BD交于P，根據同弧所對的圓心角是圓周角的二倍求出∠1=∠2=60°，證明AC⊥BD，根據直角三角形30°的性質得出：PD=$\frac{1}{2}$d，AP=$\frac{\sqrt{3}}{2}$d，PC=$\frac{1}{2}$b，PB=$\frac{\sqrt{3}}{2}$b；并利用兩角對應相等證明△APB∽△DPC，列比例式$\frac{AP}{PD}=\frac{AB}{DC}$，代入后可得：a=$\sqrt{3}$c，由勾股定理得4c²=b²+d²，代入四邊形ABCD的面積公式可得結論．

解答 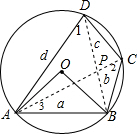解：連接AC，BD交于P，
∵∠AOB=120°，
∴∠1=∠2=60°，
∵∠ABC=97.5°，
∴∠3=22.5°，
∵∠DAB=52.5°，
∴∠DAC=30°，
∴∠1+∠DAC=90°，
∴AC⊥BD，
在Rt△ADP中，∵∠DAC=30°，AD=d，
∴PD=$\frac{1}{2}$d，AP=$\frac{\sqrt{3}}{2}$d，
同理得：PC=$\frac{1}{2}$b，PB=$\frac{\sqrt{3}}{2}$b，
∵∠BAC=∠BDC，∠APB=∠DPC，
∴△APB∽△DPC，
∴$\frac{AP}{PD}=\frac{AB}{DC}$，
∴$\frac{\frac{\sqrt{3}}{2}d}{\frac{1}{2}d}$=$\frac{a}{c}$，
∴a=$\sqrt{3}$c，
在Rt△CPD中，由勾股定理得：DC²=PD²+PC²，
c²=$（\frac{1}{2}d）^{2}+（\frac{1}{2}b）^{2}$，
4c²=b²+d²，
∴S_{四邊形ABCD}=$\frac{1}{2}$AC•BD=$\frac{1}{2}$（AP+PC）（BP+PD），
=$\frac{1}{2}$（$\frac{\sqrt{3}}{2}$d+$\frac{1}{2}$b）（$\frac{\sqrt{3}}{2}$b+$\frac{1}{2}$d），
=$\frac{1}{8}$（$\sqrt{3}$d²+4bd+$\sqrt{3}$b²），
=$\frac{1}{8}$[$\sqrt{3}$（b²+d²）+4bd]，
=$\frac{1}{8}$（4$\sqrt{3}$c²+4bd），
=$\frac{1}{8}$（4ac+4bd），
=$\frac{1}{2}$（ac+bd）．

點評 本題是圓內接四邊形，考查了圓內接四邊形的對角互補、圓周角定理、勾股定理及四邊形的面積等知識，明確對角線互相垂直的四邊形的面積等于兩條對角線乘積的一半，本題比較復雜，根據相似三角形和勾股定理將對角線轉化為四邊，從而使問題得以解決．