
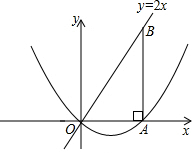
 如圖,在平面直角坐標系中,點B在直線y=2x上,過點B作x軸的垂線,垂足為A,OA=5,若拋物線y=x2+bx+c過O、A兩點.
如圖,在平面直角坐標系中,點B在直線y=2x上,過點B作x軸的垂線,垂足為A,OA=5,若拋物線y=x2+bx+c過O、A兩點.分析 (1)利用代入法可得二次函數的解析式;
(2)由OA=5,BA⊥x軸,可得B點橫坐標為5,將x=5代入y=2x可得y=10,即可得B點的坐標,易得C點坐標為(-5,10),將x=-5代入(1)所得解析式即可判斷.
解答 解:(1)∵OA=5,
∴A(5,0),
拋物線y=x2+bx+c過O、A兩點,
∴將O、A兩點代入拋物線y=x2+bx+c得,
∴$\left\{\begin{array}{l}{0=c}\\{\;}\\{0{=5}^{2}+5b}\end{array}\right.$
解得$\left\{\begin{array}{l}{b=-5}\\{\;}\\{c=0}\end{array}\right.$,
∴拋物線的解析式為:y=x2-5x;
(2)點C不在該拋物線上.
∵OA=5,BA⊥x軸,
∴B點橫坐標為5,
將x=5代入y=2x可得y=10
∴B點的坐標為(5,10),
∵點B關于y軸對稱的對稱點為C,
∴C點坐標為(-5,10),
當x=-5時,y=x2-5x=25+25=50≠10,
∴點C不在該拋物線上.
點評 本題主要考查了待定系數法求二次函數的解析式,利用代入法是解答此題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{9}{2}$$\sqrt{2}$ | B. | -$\frac{7}{2}$$\sqrt{2}$ | C. | $\frac{9}{\sqrt{2}}$ | D. | -$\frac{7}{\sqrt{2}}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
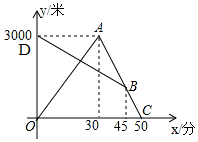 某天早晨,張強從家跑步去體育鍛煉,同時媽媽從體育場晨練結束回家,途中兩人相遇,張強跑到體育場后發現要下雨,立即按原路返回,遇到媽媽后兩人一起回到家(張強和媽媽始終在同一條筆直的公路上行走).如圖是兩人離家的距離y(米)與張強出發的時間x(分)之間的函數圖象,根據圖象信息解答下列問題:
某天早晨,張強從家跑步去體育鍛煉,同時媽媽從體育場晨練結束回家,途中兩人相遇,張強跑到體育場后發現要下雨,立即按原路返回,遇到媽媽后兩人一起回到家(張強和媽媽始終在同一條筆直的公路上行走).如圖是兩人離家的距離y(米)與張強出發的時間x(分)之間的函數圖象,根據圖象信息解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com