
 已知函數y=mx2+(2m+1)x+2(m為實數).
已知函數y=mx2+(2m+1)x+2(m為實數).分析 (1)分m=0和m≠0兩種情況討論;
(2)m=-1時y=-x2-x+2、m=1時y=x2+3x+2,畫出函數圖象,根據函數圖象得出交點;
(3)在y=mx2+(2m+1)x+2=(x+2)(mx+1)中,可知無論m為何值,x=0時y=2、x=-2時y=0,即可得.
解答 解:(1)當m=0時,y=x+2,此直線與x軸交于(-2,0);
當m≠0時,△=(2m+1)2-8m=(2m-1)2≥0,
∴此拋物線在m=$\frac{1}{2}$時,與x軸只有一個公共點;在m≠$\frac{1}{2}$時,與x軸有2個交點;
(2)當m=-1時,拋物線解析式為y=-x2-x+2,
當m=1時,拋物線解析式為y=x2+3x+2,
函數圖象如下:
由函數圖象知,兩拋物線的交點為(-2,0)和(0,2);
(3)對任意實數m,函數的圖象一定過(-2,0)和(0,2),理由如下:
在函數y=mx2+(2m+1)x+2中,
無論m為何值,當x=0時,y的值均為2,即橫過點(0,2),
∵y=mx2+(2m+1)x+2=(x+2)(mx+1),
∴當x=-2時,y的值均為0,即函數圖象橫過(-2,0),
故無論m為何值,函數的圖象(-2,0)和(0,2)兩點.
點評 本題主要考查拋物線與x軸的交點,熟練掌握拋物線與x軸交點情況取決于△的值及函數圖象的畫法、分類討論思想的運用是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 產品 | 前三天銷售總量(件) |
| 玩偶 | 720 |
| 道具 | m |
| 手環 | 300 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
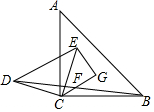 如圖,△ABC和△DEC都是等腰直角三角形,連接BD,F是BD的中點,連接CF并延長至G,使FG=CF,連接EC,CE=10,CF=4,EG=6,則S△ABC=2$\sqrt{130}$.
如圖,△ABC和△DEC都是等腰直角三角形,連接BD,F是BD的中點,連接CF并延長至G,使FG=CF,連接EC,CE=10,CF=4,EG=6,則S△ABC=2$\sqrt{130}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,拋物線y=-x2+mx+n與x軸分別交于點A(4.0),B(-2.0).與y軸交于點C
如圖,拋物線y=-x2+mx+n與x軸分別交于點A(4.0),B(-2.0).與y軸交于點C查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com