亚洲美女在线视频,国产一区二区三区欧美,91在线观看视频

精英家教網 > 初中數學 > 題目詳情

7．解方程組：
①$\left\{\begin{array}{l}{2（x-1）-y=6}\\{x=y-1}\end{array}\right.$
②$\left\{\begin{array}{l}4x-3y=11，\;\\ 2x+y=13\;.\end{array}\right.$．

分析 ①方程組利用代入消元法求出解即可；
②方程組利用加減消元法求出解即可．

解答解：①$\left\{\begin{array}{l}{2x-y=8①}\\{x=y-1②}\end{array}\right.$，
把②代入①得：2y-2-y=8，
解得：y=10，
把y=10代入②得：x=9，
則方程組的解為$\left\{\begin{array}{l}{x=9}\\{y=10}\end{array}\right.$；
②$\left\{\begin{array}{l}{4x-3y=11①}\\{2x+y=13②}\end{array}\right.$，
①+②×3得：10x=50，
解得：x=5，
把x=5代入②得：y=3，
則方程組的解為$\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$．

點評此題考查了解二元一次方程組，利用了消元的思想，消元的方法有：代入消元法與加減消元法．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：選擇題

8．

如圖，△ABC∽△BDC，BC=$\sqrt{6}$，AC=3，則CD的長為（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

18．（1）（1-π）×$\root{3}{27}$-（$\frac{1}{7}$）^-1+|-2|
（2）先化簡，再求值：$\frac{{a}^{2}-2a}{{a}^{2}-1}$÷（a-1-$\frac{2a-1}{a+1}$，其中a=3．

查看答案和解析>>

科目：初中數學 來源： 題型：選擇題

15．

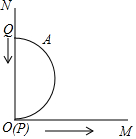如圖，己知射線OM與射線ON互相垂直，A是直徑PQ為2cm的半圓鐵片上一點，且弧AQ的度數為60°，（即弧AQ所對的圓心角為60°）動點P從點O沿射線OM開始滑動，同時動點Q在ON上滑動，當點Q滑至點O停止時，點A所經過的路程是（　　）

A．

B．

3-$\sqrt{3}$

C．

3+$\sqrt{3}$

D．

6-2$\sqrt{3}$

查看答案和解析>>

科目：初中數學 來源： 題型：選擇題

2．

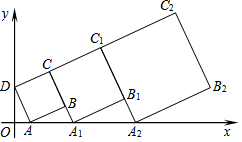在平面直角坐標系中，正方形ABCD的位置如下圖所示，點A的坐標為（1，0），點D的坐標為（0，3）．延長CB交x軸于點A₁，作正方形A₁B₁C₁C；延長C₁B₁交x軸于點A₂，作正方形A₂B₂C₂C₁…按這樣的規律進行下去，第2012個正方形的面積為（　　）

A．

$\sqrt{10}$×（$\frac{4}{3}$）⁴⁰²²

B．

10×（$\frac{4}{3}$）⁴⁰²²

C．

5×（$\frac{4}{3}$）⁴⁰²²

D．

10×（$\frac{4}{3}$）⁴⁰²³

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

12．計算：（-$\frac{3}{2}$）²÷（-$\frac{1}{2}$）²×（1$\frac{1}{3}$）²-（-4）²-4²．

查看答案和解析>>

科目：初中數學 來源： 題型：選擇題

19．如圖1，在邊長為4的正△ABC中，點P以每秒1cm的速度從點A出發，沿折線AB-BC運動，到點C停止．過點P作PD⊥AC，垂足為D，PD的長度y（cm）與點P的運動時間x（秒）的函數圖象如圖2所示．當點P運動5.5秒時，PD的長是（　　）

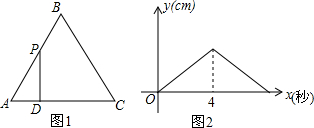
A．

$\frac{5\sqrt{3}}{4}$cm

B．

$\frac{5\sqrt{3}}{2}$cm

C．

2$\sqrt{3}$cm

D．

3$\sqrt{3}$cm

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

16．

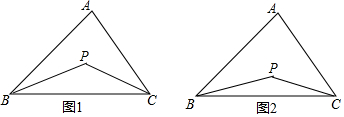【提出問題】已知如圖1，P是∠ABC、∠ACB的角平分線的交點，你能找到∠P、∠A的關系嗎？
【分析問題】在解決這個問題時，某小組同學是這樣做的：
先賦予∠A幾個特殊值：
當∠A=80°時，計算出∠P=130°；
當∠A=40°時，計算出∠P=110°；
當∠A=100°時，計算出∠P=140°；
…由以上特例猜想∠P與∠A的關系為：∠P=90°+$\frac{1}{2}$∠A．再證明這一結論：
證明：∵點P是∠ABC、∠ACB的角平分線的交點．
∴∠PBC=$\frac{1}{2}$∠ABC；∠PCB=$\frac{1}{2}$∠ACB
∴∠PBC+∠PCB=$\frac{1}{2}$（∠ABC+∠ACB）
又∵∠A+（∠ABC+∠ACB）=180°
∴∠ABC+∠ACB=180°-∠A
∴∠PBC+∠PCB=$\frac{1}{2}$（∠ABC+∠ACB）
=$\frac{1}{2}$（180°-∠A）
∴∠P=180°-（∠PBC+∠PCB）
=180°-$\frac{1}{2}$（180°-∠A）
=90°+$\frac{1}{2}$∠A
【解決問題】請運用以上解決問題的“思想方法”解決下面的幾個問題：
（1）如圖2，若點P時∠ABC、∠ACB的三等分線的交點，即∠PBC=$\frac{1}{3}$∠ABC，∠PCB=$\frac{1}{3}$∠ACB，猜測∠P與∠A的關系為∠P=$\frac{1}{3}$∠A+$\frac{2}{3}$×180°，證明你的結論．
（2）若點P時∠ABC、∠ACB的四等分線的交點，即∠PBC=$\frac{1}{4}$∠ABC，∠PCB=$\frac{1}{4}$∠ACB，則∠P與∠A的關系為∠P=$\frac{1}{4}$∠A+$\frac{3}{4}$×180°．（直接寫出答案，不需要證明）
（3）若點P時∠ABC、∠ACB的n等分線的交點，即∠PBC=$\frac{1}{n}$∠ABC，∠PCB=$\frac{1}{n}$∠ACB，則∠P與∠A的關系為$\frac{n-1}{n}$•180°+$\frac{1}{n}$∠A．（直接寫出答案，不需要證明）

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

17．解方程組：$\left\{\begin{array}{l}{x+2z=3}\\{2y+z=7}\\{2x-y-z=-5}\end{array}\right.$．

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學