
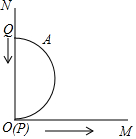
 如圖,己知射線OM與射線ON互相垂直,A是直徑PQ為2cm的半圓鐵片上一點,且弧AQ的度數為60°,(即弧AQ所對的圓心角為60°)動點P從點O沿射線OM開始滑動,同時動點Q在ON上滑動,當點Q滑至點O停止時,點A所經過的路程是( )
如圖,己知射線OM與射線ON互相垂直,A是直徑PQ為2cm的半圓鐵片上一點,且弧AQ的度數為60°,(即弧AQ所對的圓心角為60°)動點P從點O沿射線OM開始滑動,同時動點Q在ON上滑動,當點Q滑至點O停止時,點A所經過的路程是( )| A. | 3 | B. | 3-$\sqrt{3}$ | C. | 3+$\sqrt{3}$ | D. | 6-2$\sqrt{3}$ |
分析 由題意,PQ滑動過程中,PQ=2,∠QOA=30°,所以點A在射線OA上運動,起始位置時OA=$\sqrt{3}$,當P′Q′的中點在直線OA上時,OA′最長,此時OA′=2,TC AA′=2-$\sqrt{3}$,當點Q″與O重合時,OA″最小,此時OA″=1,所以點A的運動路徑為A→A′→A→A″,由此求出AA′+A′A″即可解決問題.
解答 解:如圖,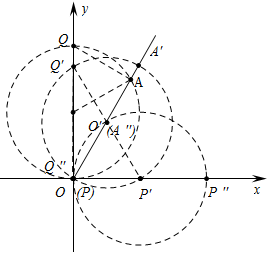
由題意,PQ滑動過程中,PQ=2,∠QOA=30°,所以點A在射線OA上運動,
起始位置時OA=$\sqrt{3}$,當P′Q′的中點在直線OA上時,OA′最長,此時OA′=2,
∴AA′=2-$\sqrt{3}$,
當點Q″與O重合時,OA″最小,此時OA″=1,
點A的運動路徑為A→A′→A→A″,
∴點A所經過的路程=2-$\sqrt{3}$+(2-1)=3-$\sqrt{3}$,
故選B.
點評 本題考查軌跡,圓心角、弦、弧之間的關系等知識,解題的關鍵是發現∠AOQ=30°,求出OA的最大值以及最小值,題目比較難,所以中考選擇題中的壓軸題.


科目:初中數學 來源: 題型:選擇題
| A. | 平均數 | B. | 中位數 | C. | 眾數 | D. | 方差 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
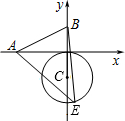 如圖,已知A、B兩點的坐標分別為(-2,0)、(0,1),⊙C的圓心坐標為(0,-1),半徑為1,E是⊙C上的一動點,則△ABE面積的最大值為( )
如圖,已知A、B兩點的坐標分別為(-2,0)、(0,1),⊙C的圓心坐標為(0,-1),半徑為1,E是⊙C上的一動點,則△ABE面積的最大值為( )| A. | 2+$\frac{\sqrt{5}}{2}$ | B. | 3+$\frac{\sqrt{5}}{2}$ | C. | 3+$\frac{\sqrt{3}}{2}$ | D. | 4+$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
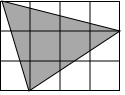 如圖由12個相同小正方形組成一個長方形.
如圖由12個相同小正方形組成一個長方形.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com