
分析 (1)根據題意畫出圖形,由直線解析式y=-x+6得點A、B的坐標,即可知OA=OB=6,從而得知∠OAB=∠OBA=45°、AB=6$\sqrt{2}$,由OC=2CA、AM=2MB得AC=2、AM=4$\sqrt{2}$、BM=2$\sqrt{2}$,根據旋轉的性質知AC=FE=2、∠MFE=∠MAC=45°,結合∠FBE=∠OBA=45°可得∠MFE=∠FBE=45°,從而知BE=FE=2,即可得出答案;
(2)作CN⊥AM于點N,由AC=2、∠OAB=45°得CN=AN=ACcos∠OAB=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$、MN=AM-AN=3$\sqrt{2}$,根據勾股定理知MC=$\sqrt{C{N}^{2}+M{N}^{2}}$=2$\sqrt{5}$,在Rt△MCN中,根據sin∠AMC=$\frac{CN}{CM}$可得答案.
解答 解:(1)如圖所示,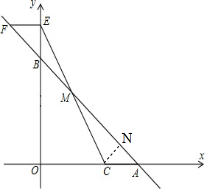
y=-x+6中,當x=0時y=6,即點B(0,6),
當y=0時-x+6=0,解得x=6,即點A(6,0),
則OA=OB=6,
∴∠OAB=∠OBA=45°,AB=6$\sqrt{2}$,
∵OC=2CA,AM=2MB,
∴AC=2,AM=4$\sqrt{2}$、BM=2$\sqrt{2}$,
∵將△ACM繞點M旋轉180°得△FEM,
∴AC=FE=2,∠MFE=∠MAC=45°,
∵∠FBE=∠OBA=45°,
∴∠MFE=∠FBE=45°,
∴BE=FE=2,
則點E的坐標為(8,0);
(2)作CN⊥AM于點N,
∵AC=2,∠OAB=45°,
∴CN=AN=ACcos∠OAB=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
則MN=AM-AN=3$\sqrt{2}$,
∴MC=$\sqrt{C{N}^{2}+M{N}^{2}}$=2$\sqrt{5}$,
∴在Rt△MCN中,sin∠AMC=$\frac{CN}{CM}$=$\frac{\sqrt{2}}{2\sqrt{5}}$=$\frac{\sqrt{10}}{10}$.
點評 本題主要考查坐標與圖形的變化-旋轉、一次函數圖象與坐標軸的交點、解直角三角形,根據題意及旋轉的性質畫出圖形,并熟練掌握旋轉的性質和解直角三角形的能力是解題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 每回投球次數 | 30 | 60 | 90 | 150 | 200 | 300 | 400 | 500 |
| 每回進球次數 | 27 | 45 | 78 | 118 | 161 | 239 | 322 | 401 |
| 進球頻率 | 0.900 | 0.750 | 0.867 | 0.787 | 0.805 | 0.797 | 0.805 | 0.802 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1cm 2cm 3cm | B. | 2cm 3cm 4cm | ||
| C. | 1cm 2cm 3.5cm | D. | 2cm 2cm 4cm |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
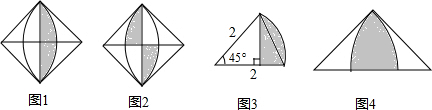
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com