
 如圖,圓O的半徑為2$\sqrt{2}$,AB、AC是圓O的兩條弦,AB=2$\sqrt{3}$,AC=4,如果以O為圓心,作一個與AC相切的圓,那么這個圓的半徑是多少?它與AB又怎樣的位置關系?為什么?
如圖,圓O的半徑為2$\sqrt{2}$,AB、AC是圓O的兩條弦,AB=2$\sqrt{3}$,AC=4,如果以O為圓心,作一個與AC相切的圓,那么這個圓的半徑是多少?它與AB又怎樣的位置關系?為什么? 分析 首先作OE⊥AC于E,連接OA,根據垂徑定理和勾股定理求出OE的長,根據直線與圓的位置關系得到答案;再求出OF的長,根據直線與圓的位置關系進行判定.
解答 解: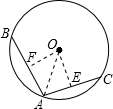 作OE⊥AC于E,連接OA,
作OE⊥AC于E,連接OA,
則AE=$\frac{1}{2}$AC=2,
則OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=2,
所以以O為圓心,作一個與直線AC相切的圓,所作的圓的半徑是2;
圓O與AB相離,理由如下:
作OF⊥AB于F,
則AF=$\frac{1}{2}$AB=$\sqrt{3}$,
∴OF=$\sqrt{O{A}^{2}-A{F}^{2}}$=$\sqrt{5}$,
∵$\sqrt{5}$>2,
∴所作的圓與直線AB相離.
點評 本題考查的是直線與圓的位置關系,如果圓心到直線的距離為d,圓的半徑為r,若d<r,則直線與圓相交;若d=r,則直線于圓相切;若d>r,則直線與圓相離.


科目:初中數學 來源:2017屆江蘇省無錫市九年級下學期第一次模擬考試數學試卷(解析版) 題型:填空題
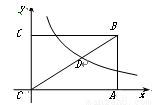
已知矩形OABC的面積為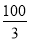 ,它的對角線OB與雙曲線
,它的對角線OB與雙曲線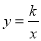 相交于點D,且OB∶OD=5∶3,則k=__________.
相交于點D,且OB∶OD=5∶3,則k=__________.
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
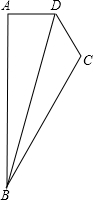 如圖,四邊形ABCD中,∠DAB=90°,AD=CD,∠BCD=∠CDA=120°,則$\frac{{S}_{△ABD}}{{S}_{△BDC}}$=$\frac{4}{3}$.
如圖,四邊形ABCD中,∠DAB=90°,AD=CD,∠BCD=∠CDA=120°,則$\frac{{S}_{△ABD}}{{S}_{△BDC}}$=$\frac{4}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 6÷(-$\frac{1}{4}$)×4=6×(-4)×4 | B. | 6÷(-$\frac{1}{4}$)×4=6×(-$\frac{1}{4}$)×4 | C. | 6÷(-$\frac{1}{4}$)×4=6÷(-$\frac{1}{4}$×4) | D. | 6÷(-$\frac{1}{4}$)×4=6×(-4)÷4 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,⊙O是△ABC的內切圓,點D,E,F為切點.
如圖,⊙O是△ABC的內切圓,點D,E,F為切點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 有兩個內角是60°的三角形 | |
| B. | 有兩邊相等且是軸對稱圖形的三角形 | |
| C. | 三邊都相等的三角形 | |
| D. | 有一個角是60°且是軸對稱圖形的三角形 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com