
分析 解方程得出x=2,再分母有理化,化簡得出原式=4x+2,最后代入求出即可.
解答 解:$\frac{x-b}{a}$=2-$\frac{x-a}{b}$,
b(x-b)=2ab-a(x-a),
bx+ax=(a+b)2,
∵a+b=2,
∴2x=4,
∴x=2,
∴$\frac{\sqrt{x+1}-\sqrt{x}}{\sqrt{x+1}+\sqrt{x}}$+$\frac{\sqrt{x+1}+\sqrt{x}}{\sqrt{x+1}-\sqrt{x}}$
=$\frac{(\sqrt{x+1}-\sqrt{x})^{2}}{(\sqrt{x+1}+\sqrt{x})(\sqrt{x+1}-\sqrt{x})}$+$\frac{(\sqrt{x+1}+\sqrt{x})^{2}}{(\sqrt{x+1}-\sqrt{x})(\sqrt{x+1}+\sqrt{x})}$
=x+1-2$\sqrt{x(x+1)}$+x+x+1+2$\sqrt{x(x+1)}$+x
=4x+2
=4×2+2
=10.
點評 本題考查了分母有理化、解一元一次方程、二次根式的化簡求出值等知識點,能正確分母有理化和求出x的值是解此題的關鍵.


科目:初中數學 來源: 題型:解答題
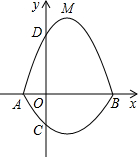 如圖所示,在平面直角坐標系中,A、B為x軸上兩點,C、D為y軸上兩點,經過點A,C,B的拋物線的一部分C1與經過點A,D,B的拋物線的一部分C2組合成一條封閉曲線,我們把這條封閉曲線稱為“蛋線”.
如圖所示,在平面直角坐標系中,A、B為x軸上兩點,C、D為y軸上兩點,經過點A,C,B的拋物線的一部分C1與經過點A,D,B的拋物線的一部分C2組合成一條封閉曲線,我們把這條封閉曲線稱為“蛋線”.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
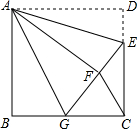 如圖,正方形ABCD中,AB=6,點E在邊CD上,且CD=3DE.將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連接AG,FC,下列結論:
如圖,正方形ABCD中,AB=6,點E在邊CD上,且CD=3DE.將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連接AG,FC,下列結論:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com