
 閱讀下面材料:數學課上,老師提出如下問題:
閱讀下面材料:數學課上,老師提出如下問題:分析 (1)根據作圖痕跡知OC=OD=BE=BF,CD=EF,證△OCD≌△BEF得∠FBE=∠AOB,從而得出答案;
(2)根據尺規作圖步驟可知.
解答 解:(1)連接CD、EF,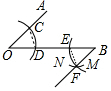
由小明的作圖知,
OC=OD=BE=BF,CD=EF,
在△OCD和△BEF中,
∵$\left\{\begin{array}{l}{OC=BE}\\{OD=BF}\\{CD=EF}\end{array}\right.$,
∴△OCD≌△BEF(SSS),
∴∠FBE=∠AOB,
∴小明的作圖依據是三邊對應相等的兩個三角形全等,全等三角形的對應角相等,
故答案為:三邊對應相等的兩個三角形全等,全等三角形的對應角相等;
(2)他所畫的痕跡弧MN是以點E為圓心,CD的長度為半徑的弧,
故答案為:E、CD.
點評 本題考查了基本作圖和全等三角形的判定與性質;由全等得到角相等是用的全等三角形的性質,熟練掌握三角形全等的性質是正確解答本題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:填空題
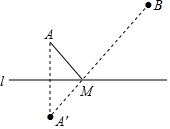 如圖,A、B兩點在直線l的同側,在l上求作一點M,使AM+BM最小.小明的做法是:做點A關于直線l的對稱點A',連結A'B,交直線l于點M,點M即為所求.請你寫出小明這樣作圖的依據:兩點確定一條直線、線段垂直平分線上點到線段兩個端點距離相等.
如圖,A、B兩點在直線l的同側,在l上求作一點M,使AM+BM最小.小明的做法是:做點A關于直線l的對稱點A',連結A'B,交直線l于點M,點M即為所求.請你寫出小明這樣作圖的依據:兩點確定一條直線、線段垂直平分線上點到線段兩個端點距離相等.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,將一個邊長為a的正方形分割成一個邊長為b的小正方形(a>b)和兩個梯形,通過兩種不同的方法計算陰影部分面積,驗證了一個等式,則這個等式是( )
如圖,將一個邊長為a的正方形分割成一個邊長為b的小正方形(a>b)和兩個梯形,通過兩種不同的方法計算陰影部分面積,驗證了一個等式,則這個等式是( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+b)(a-b)=a2-b2 | D. | (a+2b)(a-b)=a2+ab-2b2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
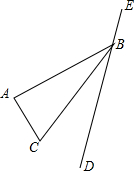 作圖題:(畫出圖形,并寫出結論)
作圖題:(畫出圖形,并寫出結論)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖甲,在邊長為a的正方形中挖去一個邊長為b的小正方形(a>b),把余下的部分剪拼成一個矩形如圖乙,通過計算兩個圖形(陰影部分)的面積,驗證了一個等式,則這個等式是( )
如圖甲,在邊長為a的正方形中挖去一個邊長為b的小正方形(a>b),把余下的部分剪拼成一個矩形如圖乙,通過計算兩個圖形(陰影部分)的面積,驗證了一個等式,則這個等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com