
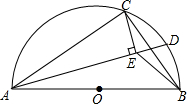
 如圖,AB是半圓O的直徑,點C在半圓O上,AB=5cm,AC=4cm.D是弧BC上的一個動點(含端點B,不含端點C),連接AD,過點C作CE⊥AD于E,連接BE,在點D移動的過程中,BE的取值范圍是$\sqrt{13}$-2≤BE<3.
如圖,AB是半圓O的直徑,點C在半圓O上,AB=5cm,AC=4cm.D是弧BC上的一個動點(含端點B,不含端點C),連接AD,過點C作CE⊥AD于E,連接BE,在點D移動的過程中,BE的取值范圍是$\sqrt{13}$-2≤BE<3. 分析 由∠AEC=90°知E在以AC為直徑的⊙M的$\widehat{CN}$上(不含點C、可含點N),從而得BE最短時,即為連接BM與⊙M的交點(圖中點E′點),作MF⊥AB于F,證△AMF∽△ABC得$\frac{MF}{BC}$=$\frac{AM}{AB}$,即可知MF=$\frac{6}{5}$、AF=$\sqrt{A{M}^{2}-M{F}^{2}}$=$\frac{8}{5}$、BF=$\frac{17}{5}$、BM=$\sqrt{13}$,從而得BE長度的最小值BE′=BM-ME′=$\sqrt{13}$-2;由BE最長時即E與C重合,根據BC=3且點E與點C不重合,得BE<3,從而得出答案.
解答 解:如圖,
由題意知,∠AEC=90°,
∴E在以AC為直徑的⊙M的$\widehat{CN}$上(不含點C、可含點N),
∴BE最短時,即為連接BM與⊙M的交點(圖中點E′點),
∵AB=5,AC=4,
∴BC=3,
作MF⊥AB于F,
∴∠AFM=∠ACB=90°,∠FAM=∠CAB,
∴△AMF∽△ABC,
∴$\frac{MF}{BC}$=$\frac{AM}{AB}$,即$\frac{MF}{3}=\frac{2}{5}$,得MF=$\frac{6}{5}$,
∴AF=$\sqrt{A{M}^{2}-M{F}^{2}}$=$\frac{8}{5}$,
則BF=AB-AF=$\frac{17}{5}$,
∴BM=$\sqrt{M{F}^{2}+B{F}^{2}}$=$\sqrt{13}$,
∴BE長度的最小值BE′=BM-ME′=$\sqrt{13}$-2,
BE最長時,即E與C重合,
∵BC=3,且點E與點C不重合,
∴BE<3,
綜上,$\sqrt{13}$-2≤BE<3,
故答案為:$\sqrt{13}$-2≤BE<3.
點評 本題主要考查圓周角定理、勾股定理、相似三角形的判定與性質等知識點,根據題意得出BE最短時,即為連接BM與⊙M的交點是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| 身高(cm) | 172 | 173 | 175 | 176 |
| 人數(個) | 4 | 4 | 4 | 4 |
| A. | 173cm,173cm | B. | 174cm,174cm | C. | 173cm,174cm | D. | 174cm,175cm |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,將△ABC繞點C順時針旋轉90°后得到△A′B′C′,則點A的對應點A′的坐標為( )
如圖,將△ABC繞點C順時針旋轉90°后得到△A′B′C′,則點A的對應點A′的坐標為( )| A. | (0,$\sqrt{2}$) | B. | (0,-3) | C. | (-1,0) | D. | (3,0) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
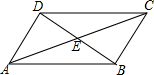 如圖,在四邊形ABCD中,對角線AC、BD相交于點E,∠CBD=90°,BC=4,BE=ED=3,AC=10,則四邊形ABCD的面積為24.
如圖,在四邊形ABCD中,對角線AC、BD相交于點E,∠CBD=90°,BC=4,BE=ED=3,AC=10,則四邊形ABCD的面積為24.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 為了響應國家節能減排的號召,鼓勵市民節約用電,我市從2016年7月1日起,居民用電實行“一戶一表”的“階梯電價”,分三個檔次收費,第一檔是用電量不超過180千瓦時實行“基本電價”,第二、三檔實行“提高電價”,具體收費情況見折線圖,請根據圖象回答下列問題:
為了響應國家節能減排的號召,鼓勵市民節約用電,我市從2016年7月1日起,居民用電實行“一戶一表”的“階梯電價”,分三個檔次收費,第一檔是用電量不超過180千瓦時實行“基本電價”,第二、三檔實行“提高電價”,具體收費情況見折線圖,請根據圖象回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com