
 如圖,△ABC中,AB=AC,D為AB中點,E在AC上,且BE⊥AC,若DE=5,AE=8,則BC的長度為2$\sqrt{10}$.
如圖,△ABC中,AB=AC,D為AB中點,E在AC上,且BE⊥AC,若DE=5,AE=8,則BC的長度為2$\sqrt{10}$. 分析 由BE⊥AC,D為AB中點,DE=5,根據直角三角形斜邊的中線等于斜邊的一半,即可求得AB的長,然后由勾股定理求得BC的長.
解答 解:∵BE⊥AC,
∴∠AEB=90°,
∵D為AB中點,
∴AB=2DE=2×5=10,
∵AE=8,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=6.
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$,
故答案為:2$\sqrt{10}$.
點評 此題考查了直角三角形斜邊上的中線的性質以及勾股定理.注意掌握直角三角形斜邊的中線等于斜邊的一半定理的應用是解此題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,矩形OABC的兩邊OA,OC分別在x軸、y軸的正半軸上,OA=4,OC=2,點P從點O出發,沿x軸以每秒1個單位的速度向點A勻速運動,到達點A時停止運動,設點P運動的時間是t秒(t>0),過點P作∠DPA=∠CPO,且PD=$\frac{1}{2}$CP,連接DA.
如圖,在平面直角坐標系中,矩形OABC的兩邊OA,OC分別在x軸、y軸的正半軸上,OA=4,OC=2,點P從點O出發,沿x軸以每秒1個單位的速度向點A勻速運動,到達點A時停止運動,設點P運動的時間是t秒(t>0),過點P作∠DPA=∠CPO,且PD=$\frac{1}{2}$CP,連接DA.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC中,AD是△ABC的邊BC上的高,E、F分別是AB、AC的中點,AC=13、AB=20、BC=21.
如圖,△ABC中,AD是△ABC的邊BC上的高,E、F分別是AB、AC的中點,AC=13、AB=20、BC=21.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
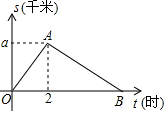 平頂山市教育局舉行'重走長征路”健步活動,某教師從起點體育村沿建設路到市生態園.再沿原路返回.該教師離開起點的路程S(千米)與步行時間t(小時)之間的函數關系如圖所示.其中從起點到市生態園的平均速度是4千米/小時.用2小時.根據圖象提供信息.解答下列問題
平頂山市教育局舉行'重走長征路”健步活動,某教師從起點體育村沿建設路到市生態園.再沿原路返回.該教師離開起點的路程S(千米)與步行時間t(小時)之間的函數關系如圖所示.其中從起點到市生態園的平均速度是4千米/小時.用2小時.根據圖象提供信息.解答下列問題查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com