
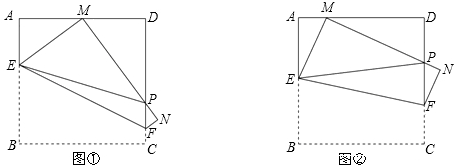
分析 (1)①依據兩組角對應相等的三角形相似可證明△AEM∽△DMP,△PFN∽△PMD,然后依據兩組邊對應成比例且夾角相等的兩個三角形相似證明△EMP∽△MDP即可;②設AE=x,則EM=4-x,在Rt△AEM中,依據勾股定理可求得x的值,然后可求得△AEM的周長,然后依據相似三角形的周長比等于相似比求解即可;
(2)設AM=m,AE=n,則DM=4-m,EM=4-n.在Rt△AEM中,依據勾股定理和完全平方公式可得到8n=16-m2,然后可△PMD∽△MEA可求得△PMD的周長.
解答 解:(1)①依據翻折的性質可知∠EMP=∠B=90°,∠C=∠N=90°
∴∠AME+∠PMD=90°.
又∵∠AME+∠AEM=90°,
∴∠AEM=∠PMD.
又∵∠A=∠D,
∴△AME∽△DPM.
∵∠MPD=∠FPN,∠D=∠N=90°
∴△MPD∽△FPN.
∵△AME∽△DPM,
∴$\frac{AM}{ME}=\frac{DP}{MP}$.
又∵AM=MD,
∴$\frac{DM}{ME}=\frac{DP}{MP}$.
又∵∠EMP=∠D=90°,
∴△EMP∽△MDP.
故答案為:△AME∽△DPM,△AME∽△DPM,△EMP∽△MDP.
②∵四邊形ABCD是正方形,
∴AD=AB=4.
∵點M是AD邊中點,
∴AM=DM=2.
由折疊的性質得:ME=BE,
∴△MEA的周長為6.
在Rt△MEA中,設AE=x,則ME=4-x.
∴x2+22=(4-x)2,解得:x=$\frac{3}{2}$.
∵△PMD∽△MEA,
∴$\frac{△PMD的周長}{△MEA的周長}$=$\frac{DM}{AE}$=$\frac{4}{3}$,即$\frac{△PMD的周長}{6}=\frac{4}{3}$.
∴△PMD的周長為8.
(2)△PMD的周長不變.
設AM=m,AE=n,則DM=4-m,EM=4-n,△AEM的周長=4+m.
在Rt△AME中,依據勾股定理可知:m2+n2=(4-n)2,即8n=16-m2.
∵△PMD∽△MEA,
∴$\frac{△PMD的周長}{△MEA的周長}$=$\frac{DM}{AE}$$\frac{4-m}{n}$.
∴△PMD的周長=$\frac{(4-m)(4+m)}{n}$=$\frac{16-{m}^{2}}{n}$=$\frac{8n}{8}$=8.
點評 本題主要考查的是相似三角形的綜合應用,解答本題主要應用了相似三角形的性質和判定,翻折的性質、勾股定理的應用,熟練掌握相似三角形的性質是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 第17個數 | B. | 第18個數 | C. | 第19個數 | D. | 第20個數 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
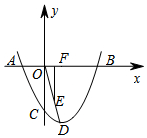 如圖,一拋物線經過點A(-2,0),B(6,0),C(0,-3),D為拋物線的頂點,過OD的中點E,作EF⊥x軸于點F,G為x軸上一動點,M為拋物線上一動點,N為直線EF上一動點,當以F、G、M、N為頂點的四邊形是正方形時,點G的坐標為(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).
如圖,一拋物線經過點A(-2,0),B(6,0),C(0,-3),D為拋物線的頂點,過OD的中點E,作EF⊥x軸于點F,G為x軸上一動點,M為拋物線上一動點,N為直線EF上一動點,當以F、G、M、N為頂點的四邊形是正方形時,點G的坐標為(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com