Question

1．已知，在平面直角坐標(biāo)系中，點(diǎn)D的坐標(biāo)為（a，b），且a，b滿足a²-12a+36+$\sqrt{a-b}$=0，E，F(xiàn)分別為x軸，y軸的正半軸上一點(diǎn)，∠EDF=45°．
（1）求a，b的值；
（2）如圖1，過E作EG⊥DF于點(diǎn)G，若點(diǎn)E的坐標(biāo)為（0，2），求點(diǎn)G的坐標(biāo)；
（3）如圖2，過E作EP∥x軸交DF于點(diǎn)P，當(dāng)E，F(xiàn)運(yùn)動時(shí)，求證：PE+OE+OF=定值．

Answer 1

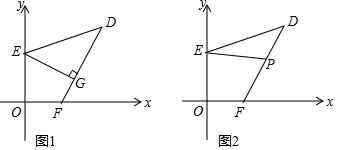
分析 （1）利用非負(fù)性的特征即可求出a，b的值，
（2）先判斷出△AEG≌△BGD得出AG=BD，OA=BG，即可得出點(diǎn)G的縱橫坐標(biāo)的關(guān)系，再用勾股定理即可求出點(diǎn)G的坐標(biāo)；
（3）構(gòu)造出如圖所示圖形，再判斷出四邊形EFCP為菱形，最后用等量代換即可得出結(jié)論．

解答 解：（1）∵a²-12a+36+$\sqrt{a-b}$=0，
∴（a-6）²+$\sqrt{a-b}$=0，
∴a=b=6，
（2）如圖1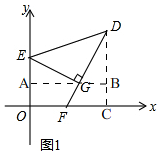，過點(diǎn)D作DC⊥x軸，過點(diǎn)G作AB∥x軸，交y軸于A，
∴∠DBG=90°，
∵∠DGE=90°，
∴EG=DG，∠AGE+∠BGD=90°，
∵∠AGE+∠AEG=90°，
∴∠AEG=∠BGD，
在△AEG和△BGD中，$\left\{\begin{array}{l}{∠EAG=∠GBD}\\{∠AEG=∠BGD}\\{EG=DG}\end{array}\right.$，
∴△AEG≌△BGD，
∴AG=BD，OA=BG，
設(shè)G的橫坐標(biāo)為h，則G的縱坐標(biāo)為6-h，
∴AG=h，OA=6-h，
∵E（0，2），
∴OE=2，
∴AE=OE-OA=2-（6-h）=h-4，
∵D（6，6），E（0，2），
∴DE=2$\sqrt{13}$，
在Rt△DEG中，EG²=$\frac{1}{2}$DE²=26，
在Rt△AEG中，AE²+AG²=EG²，
∴（h-4）²+h²=26，
∴h=-1（舍）或h=5，
∴OA=1，∴G（5，1）；
（3）如圖2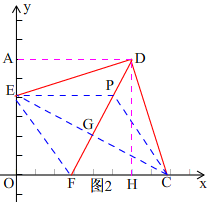，過點(diǎn)D作DA⊥OE，將△ADE繞點(diǎn)D逆時(shí)針旋轉(zhuǎn)90°，
而AD=DH=6，所以旋轉(zhuǎn)得到如圖2所示的△DHC，
∴DE=DC，∠ADE=∠HDC，
∴∠CDE=90°，
∵∠EDF=45°，
∴∠CDF=45°，
連接CE，
∴DF⊥EC，
∴DF是線段EC的垂直平分線上的點(diǎn)，
∴PE=PC，F(xiàn)E=FC，
∴∠PEC=∠PCE，
∵PE∥x軸，
∴∠PEC=∠OCE=∠PCE，
∵CE⊥PF，
∴CP=CF，
∴PE=EF=CF=PC，
∴四邊形PEFC是菱形，
∴PE=CF，
∴PE+OE+OF=CF+OE+OF=OC+OE=OH+CH+OE=OH+AE+OE=OH+OA=6+6=12，
即：PE+OE+OF=定值=12．

點(diǎn)評 此題是三角形綜合題，主要考查了非負(fù)性，全等三角形的判定和性質(zhì)，旋轉(zhuǎn)的性質(zhì)，勾股定理，等腰直角三角形的性質(zhì)，解本題的關(guān)鍵是判斷出△AEG≌△BGD，構(gòu)造出圖形是解本題的難點(diǎn)，是一道很好的中考常考題．