Question

6．已知二次函數y=-x²+2x+3，點P（t，0）是x軸上的動點，設Q（0，2t）是y軸上的動點，線段PQ與函數y=-|x|²+2|x|+3只有一個公共點，求t的取值．

Answer 1

分析 （1）先將函數y=-|x|²+2|x|+3的解析式去掉絕對值，變形為：y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3（x≥0）}\\{-{x}^{2}-2x+3（x＜0）}\end{array}\right.$，
（2）利用待定系數法求線段PQ的解析式；
（3）分情況進行討論：
①當線段PQ過（0，3）和過（3，0）時，計算出t的值，利用圖形得出t的取值；
②將y=-2x+2t代入y=-x²+2x+3（x≥0）中得，根據△=0得出t的值；
③當線段PQ過B（-3，0），如圖3，同理得出t的取值．

解答 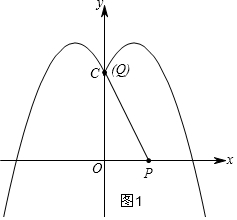解：函數y=-|x|²+2|x|+3的解析式可化為：
y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3（x≥0）}\\{-{x}^{2}-2x+3（x＜0）}\end{array}\right.$，
設線段PQ所在的直線的解析式為：y=kx+b，
將P（t，0）、Q（0，2t）代入得：$\left\{\begin{array}{l}{tk+b=0}\\{b=2t}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-2}\\{b=2t}\end{array}\right.$，
∴線段PQ所在的直線的解析式為：y=-2x+2t；
①當線段PQ過（0，3）時，即點Q與C重合，如圖1，
2t=3，
t=$\frac{3}{2}$，
∴當t=$\frac{3}{2}$時，線段PQ與函數y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3（x≥0）}\\{-{x}^{2}-2x+3（x＜0）}\end{array}\right.$只有一個公共點；
當線段PQ過（3，0）時，即點P與A（3，0）重合，如圖2，
t=3，
此時線線段PQ與函數y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3（x≥0）}\\{-{x}^{2}-2x+3（x＜0）}\end{array}\right.$有兩個公共點
，
∴當$\frac{3}{2}$≤t＜3時，線段PQ與函數y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3（x≥0）}\\{-{x}^{2}-2x+3（x＜0）}\end{array}\right.$只有一個公共點；
②將y=-2x+2t代入y=-x²+2x+3（x≥0）中得，
-x²+2x+3=-2x+2t，
-x²+4x+3-2t=0，
△=16-4×（-1）×（3-2t）=28-8t=0，
t=$\frac{7}{2}$，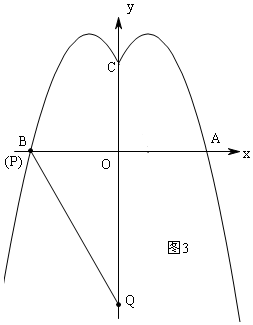
∴當t=$\frac{7}{2}$時，線段PQ與函數y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3（x≥0）}\\{-{x}^{2}-2x+3（x＜0）}\end{array}\right.$也只有一個公共點；
③當線段PQ過B（-3，0），如圖3，即P與B（-3，0）重合，線段PQ只與y=-x²-2x+3（x＜0）有一個公共點，此時t=-3，
∴當t≤-3時，線段PQ與函數y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3（x≥0）}\\{-{x}^{2}-2x+3（x＜0）}\end{array}\right.$也只有一個公共點；
綜上所述，當線段PQ與函數y=-|x|²+2|x|+3只有一個公共點時，t的取值是$\frac{3}{2}$≤t＜3或t=$\frac{7}{2}$或t≤-3．

點評 本題考查了兩個二次函數組合的復合函數的取值問題，難度較大；利用數形結合的思想，從特殊位置著手，并注意是線段與函數有一個交點，采用了分類討論的思想解決此題．