
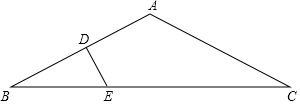
 如圖,△ABC中,AB=AC=2$\sqrt{5}$,BC=8,AB的垂直平分線交AB于點(diǎn)D,交BC于點(diǎn)E,設(shè)△BDE的面積為S1,四邊形ADEC的面積為S2,則$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$.
如圖,△ABC中,AB=AC=2$\sqrt{5}$,BC=8,AB的垂直平分線交AB于點(diǎn)D,交BC于點(diǎn)E,設(shè)△BDE的面積為S1,四邊形ADEC的面積為S2,則$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$. 分析 過(guò)A作AE⊥BC于E,根據(jù)等腰三角形的性質(zhì)得到BE=CE=4,由DE垂直平分AB,得到BD=$\frac{1}{2}$AB=$\sqrt{5}$,根據(jù)相似三角形的性質(zhì)得到$\frac{{S}_{△BED}}{{S}_{△ABE}}$=($\frac{BD}{BE}$)2=$\frac{5}{16}$,求得$\frac{{S}_{△BED}}{{S}_{△ABC}}$=$\frac{5}{32}$,于是得到結(jié)論.
解答 解:過(guò)A作AE⊥BC于E,
∵AB=AC=2$\sqrt{5}$,BC=8,
∴BE=CE=4,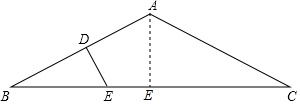
∵DE垂直平分AB,
∴BD=$\frac{1}{2}$AB=$\sqrt{5}$,
∵∠BDE=∠AEB=90°,∠B=∠B,
∴△BED∽△ABE,
∴$\frac{{S}_{△BED}}{{S}_{△ABE}}$=($\frac{BD}{BE}$)2=$\frac{5}{16}$,
∵S△ABC=2S△ABE,
∴$\frac{{S}_{△BED}}{{S}_{△ABC}}$=$\frac{5}{32}$,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{27}$.
故答案為:$\frac{5}{27}$.
點(diǎn)評(píng) 本題考查了相似三角形的判定和性質(zhì),等腰三角形的性質(zhì),線段垂直平分線的性質(zhì),正確的作出輔助線是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
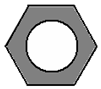 如圖,六角螺母的橫截面是正六邊形,它的每條邊都相等,每個(gè)內(nèi)角也都相等.求這個(gè)六邊形的每一個(gè)內(nèi)角的度數(shù).
如圖,六角螺母的橫截面是正六邊形,它的每條邊都相等,每個(gè)內(nèi)角也都相等.求這個(gè)六邊形的每一個(gè)內(nèi)角的度數(shù).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
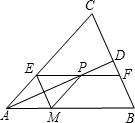 如圖,等腰△ABC中,AB=AC,AD平分∠BAC交BC于D,在線段AD上任取一點(diǎn)P(點(diǎn)A除外),過(guò)點(diǎn)P作EF∥AB,分別交AC、BC于E,F(xiàn)點(diǎn),作PM∥AC,交AB于M點(diǎn),連接ME.
如圖,等腰△ABC中,AB=AC,AD平分∠BAC交BC于D,在線段AD上任取一點(diǎn)P(點(diǎn)A除外),過(guò)點(diǎn)P作EF∥AB,分別交AC、BC于E,F(xiàn)點(diǎn),作PM∥AC,交AB于M點(diǎn),連接ME.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
| -2 | -4 | 3x+6 |
| 4 | x | |
| -x-6 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
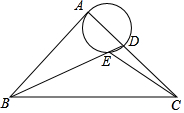 如圖,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2$\sqrt{2}$,點(diǎn)D是AC邊上一動(dòng)點(diǎn),連接BD,以AD為直徑的圓交BD于點(diǎn)E,則線段CE長(zhǎng)度的最小值為( )
如圖,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2$\sqrt{2}$,點(diǎn)D是AC邊上一動(dòng)點(diǎn),連接BD,以AD為直徑的圓交BD于點(diǎn)E,則線段CE長(zhǎng)度的最小值為( )| A. | 2$\sqrt{2}$-2 | B. | $\sqrt{5}-2$ | C. | $\sqrt{5}-1$ | D. | $\sqrt{3}-1$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 1個(gè) | B. | 2個(gè) | C. | 3個(gè) | D. | 4個(gè) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
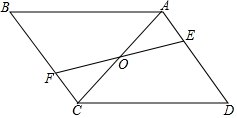 已知:如圖,平行四邊形 ABCD中,點(diǎn)E、F分別在AD、BC上,且ED=BF,EF與AC相交于點(diǎn)O.
已知:如圖,平行四邊形 ABCD中,點(diǎn)E、F分別在AD、BC上,且ED=BF,EF與AC相交于點(diǎn)O.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
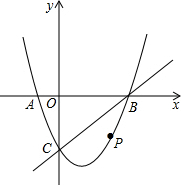 如圖,在平面直角坐標(biāo)系中,二次函數(shù)y=x2-2x-3的圖象與x軸交于A、B兩點(diǎn),A點(diǎn)在原點(diǎn)的左側(cè),B點(diǎn)在原點(diǎn)右側(cè),與y軸交于C點(diǎn),點(diǎn)P是x軸下方的拋物線上的一動(dòng)點(diǎn).
如圖,在平面直角坐標(biāo)系中,二次函數(shù)y=x2-2x-3的圖象與x軸交于A、B兩點(diǎn),A點(diǎn)在原點(diǎn)的左側(cè),B點(diǎn)在原點(diǎn)右側(cè),與y軸交于C點(diǎn),點(diǎn)P是x軸下方的拋物線上的一動(dòng)點(diǎn).查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com