
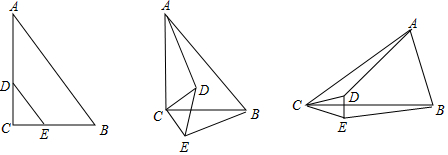
分析 (1)利用線段間的和差關(guān)系求得BE=AD;
(2)在△BCE和△ACD中,根據(jù)BC=AC,∠BCE=∠ACD,CE=CD,得出△BCE≌△ACD,從而證出BE=AD;
(3)同(2)的方法即可.
解答 解:(1)如圖1,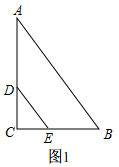
∵CA=CB,CD=CE,
∴BE=AD,
(2)AD=BE,如圖2,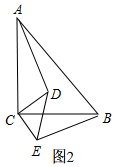
理由:∵∠ACD=∠ACB-∠DCB,∠ACB=∠DCE=90°,
∴∠ACD=∠DCE-∠DCB
∵∠BCE=∠DCE-∠DCB,
∴∠ACD=∠BCE,
在△ACD 和△BCE中,$\left\{\begin{array}{l}{CA=CB}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE.
∴AD=BE.
(3)AD=BE還成立.
如圖3,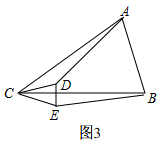
理由:∵∠ACD=∠ACB-∠DCB,∠ACB=∠DCE,
∴∠ACD=∠DCE-∠DCB
∵∠BCE=∠DCE-∠DCB,
∴∠ACD=∠BCE
在△ACD 和△BCE中,$\left\{\begin{array}{l}{CA=CB}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE.
∴AD=BE.
點評 此題是三角形綜合題,主要考查了等腰直角三角形和等腰三角形的性質(zhì);熟練運用旋轉(zhuǎn)的性質(zhì),全等三角形的判斷與性質(zhì),解題的關(guān)鍵是△ACD≌△BCE,是一道比較簡單的題目.


科目:初中數(shù)學(xué) 來源: 題型:解答題
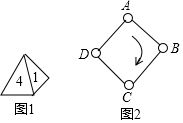 如圖1,一枚質(zhì)地均勻的正四面體骰子,它有四個面并分別標(biāo)有數(shù)字1,2,3,4,如圖2,正方形ABCD頂點處各有一個圈,跳圈游戲的規(guī)則為:游戲者每擲一次骰子,骰子著地一面上的數(shù)字是幾,就沿正方形的邊順時針方向連續(xù)跳幾個邊長.
如圖1,一枚質(zhì)地均勻的正四面體骰子,它有四個面并分別標(biāo)有數(shù)字1,2,3,4,如圖2,正方形ABCD頂點處各有一個圈,跳圈游戲的規(guī)則為:游戲者每擲一次骰子,骰子著地一面上的數(shù)字是幾,就沿正方形的邊順時針方向連續(xù)跳幾個邊長.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
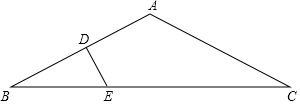 如圖,△ABC中,AB=AC=2$\sqrt{5}$,BC=8,AB的垂直平分線交AB于點D,交BC于點E,設(shè)△BDE的面積為S1,四邊形ADEC的面積為S2,則$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$.
如圖,△ABC中,AB=AC=2$\sqrt{5}$,BC=8,AB的垂直平分線交AB于點D,交BC于點E,設(shè)△BDE的面積為S1,四邊形ADEC的面積為S2,則$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | k>0 | B. | k>1 | C. | k<1 | D. | k≥1 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com