
 已知線段AB=12,CD=6,線段CD在直線AB上運動(A在B的左側,C在D的左側).
已知線段AB=12,CD=6,線段CD在直線AB上運動(A在B的左側,C在D的左側).分析 (1)根據題意即可得到結論;
(2)由(1)得AC=$\frac{1}{2}$AB,CD=$\frac{1}{2}$AB,根據線段的和差即可得到結論;
(3)需要分類討論:①如圖1,當點C在點B的右側時,根據“M、N分別為線段AC、BD的中點”,先計算出AM、DN的長度,然后計算MN=AD-AM-DN;②如圖2,當點C位于點B的左側時,利用線段間的和差關系求得MN的長度.
解答 解:(1)當D點與B點重合時,AC=AB-CD=6;
故答案為:6;
(2)由(1)得AC=$\frac{1}{2}$AB,
∴CD=$\frac{1}{2}$AB,
∵點P是線段AB延長線上任意一點,
∴PA+PB=AB+PB+PB,PC=CD+PB=$\frac{1}{2}$AB+PB,
∴PA+PB-2PC=AB+PB+PB-2($\frac{1}{2}$AB+PB)=0;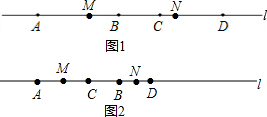 (3)如圖1,∵M、N分別為線段AC、BD的中點,
(3)如圖1,∵M、N分別為線段AC、BD的中點,
∴AM=$\frac{1}{2}$AC=$\frac{1}{2}$(AB+BC)=8,
DN=$\frac{1}{2}$BD=$\frac{1}{2}$(CD+BC)=5,
∴MN=AD-AM-DN=9;
如圖2,∵M、N分別為線段AC、BD的中點,
∴AM=$\frac{1}{2}$AC=$\frac{1}{2}$(AB-BC)=4,
DN=$\frac{1}{2}$BD=$\frac{1}{2}$(CD-BC)=1,
∴MN=AD-AM-DN=12+6-4-4-1=9.
點評 本題考查了一元一次方程的應用,比較線段的長短.利用中點性質轉化線段之間的倍分關系是解題的關鍵.


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
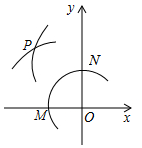 如圖,在平面直角坐標系中,以O為圓心,適當長為半徑畫弧,交x軸于點M,交y軸于點N,再分別以點M、N為圓心,大于$\frac{1}{2}$MN的長為半徑畫弧,兩弧在第二象限交于點P.若點P的坐標為(2a,b+1),則a與b的數量關系為( )
如圖,在平面直角坐標系中,以O為圓心,適當長為半徑畫弧,交x軸于點M,交y軸于點N,再分別以點M、N為圓心,大于$\frac{1}{2}$MN的長為半徑畫弧,兩弧在第二象限交于點P.若點P的坐標為(2a,b+1),則a與b的數量關系為( )| A. | a=b | B. | 2a-b=1 | C. | 2a+b=-1 | D. | 2a+b=1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 圖象中所反應的過程是:張強從家跑步去體育場,在那里鍛煉了一陣后,又去早餐店吃早餐,然后散步走回家,其中x表示時間,y表示張強離家的距離,根據圖象提供的信息,以下四個說法錯誤的是( )
圖象中所反應的過程是:張強從家跑步去體育場,在那里鍛煉了一陣后,又去早餐店吃早餐,然后散步走回家,其中x表示時間,y表示張強離家的距離,根據圖象提供的信息,以下四個說法錯誤的是( )| A. | 體育場離張強家2.5千米 | |
| B. | 張強在體育場鍛煉了15分鐘 | |
| C. | 體育場離早餐店4千米 | |
| D. | 張強從早餐店回家的平均速度是$\frac{18}{7}$千米/小時 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
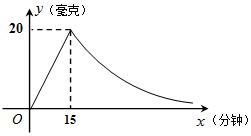 為了預防流感,某學校用藥熏消毒法對教室進行消毒.已知一瓶藥物釋放過程中,室內每立方米空氣中的含藥量y(毫克)與時間x(分鐘)成正比例;藥物釋放完畢后,y與x成反比例,如圖所示.根據圖中提供的信息,解答下列問題:
為了預防流感,某學校用藥熏消毒法對教室進行消毒.已知一瓶藥物釋放過程中,室內每立方米空氣中的含藥量y(毫克)與時間x(分鐘)成正比例;藥物釋放完畢后,y與x成反比例,如圖所示.根據圖中提供的信息,解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 32,28 | B. | 28,32 | C. | 28,28 | D. | 30,28 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com