
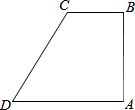
 如圖,在四邊形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P為四邊形ABCD邊上的任意一點,當∠BPC=30°時,CP的長為2或2$\sqrt{3}$或4.
如圖,在四邊形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P為四邊形ABCD邊上的任意一點,當∠BPC=30°時,CP的長為2或2$\sqrt{3}$或4. 分析 如圖,連接AC.首先證明△ACD是等邊三角形,分三種情形討論即可解決問題.
解答 解:如圖,連接AC.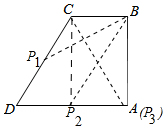
∵BC∥AD,∠DCB=120°,
∴∠D+∠DCB=180°,
∴∠D=60°,
∵DC=DA,
∴△ACD是等邊三角形,
∴∠DAC=60°,
∵AB⊥BC,
∴∠CBA=∠BAD=90°,
∴∠BAC=30°,
∴當P3與A重合時,∠BP3C=30°,此時CP3=4,
作CP2⊥AD于P2,則四邊形BCP2A是矩形,
易知∠CP2B=30°,此時CP2=2$\sqrt{3}$,
當CB=CP1時,∠CP1B=∠CBP1=30°,此時CP1=2,
綜上所述,CP的長為2或2$\sqrt{3}$或4.
故答案為2或2$\sqrt{3}$或4.
點評 本題考查等邊三角形的判定、矩形的判定、30度的直角三角形的性質、勾股定理等知識,解題的關鍵是學會用分類討論的思想思考問題,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
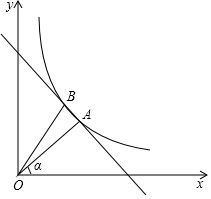 如圖,在坐標系中,線段OA在第一象限,OA=5,OA與x軸的夾角α的正切tanα=$\frac{3}{4}$,反比例函數y=$\frac{k}{x}$(k≠0,x>0)圖象經過點A,OA繞點O旋轉后落在反比例函數y=$\frac{k}{x}$(x>0)的圖象上另一點B,點B與x軸距離是4.
如圖,在坐標系中,線段OA在第一象限,OA=5,OA與x軸的夾角α的正切tanα=$\frac{3}{4}$,反比例函數y=$\frac{k}{x}$(k≠0,x>0)圖象經過點A,OA繞點O旋轉后落在反比例函數y=$\frac{k}{x}$(x>0)的圖象上另一點B,點B與x軸距離是4.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
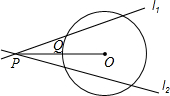 如圖,點P為⊙O外一點,連結OP交⊙O于點Q,且PQ=OQ,經過點P的直線l1,l2,都與⊙O相交,則l1與l2所成的銳角α的取值范圍是( )
如圖,點P為⊙O外一點,連結OP交⊙O于點Q,且PQ=OQ,經過點P的直線l1,l2,都與⊙O相交,則l1與l2所成的銳角α的取值范圍是( )| A. | 0°<α<30° | B. | 0°<α<45° | C. | 0°<α<60° | D. | 0°<α<90° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
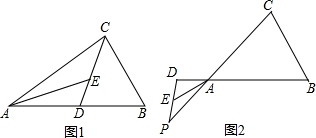
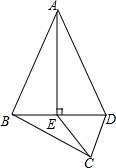 如圖,四邊形ABCD中,AB=AD,AE⊥BD于點E,連接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的長度是( )
如圖,四邊形ABCD中,AB=AD,AE⊥BD于點E,連接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的長度是( )| A. | 5 | B. | 8 | C. | 10 | D. | 無法計算 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 第一次 | 第二次 | |
| 甲種貨車輛數(單位:輛) | 2 | 5 |
| 乙種貨車輛數(單位:輛) | 3 | 6 |
| 累計貨運噸數(單位:噸) | 15.5 | 35 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com