
| 甲 | 乙 | |
| 進價(元/件) | 20 | 30 |
| 售價(元/件) | 29 | 40 |
分析 (1)設第一次購進甲種商品x件,則乙的件數(shù)為($\frac{1}{2}$x+15)件,根據總進價=甲種商品單件進價×數(shù)量+乙種商品單件進價×數(shù)量即可得出關于x的一元一次方程,解之即可得出x的值,再根據總利潤=甲種商品單件利潤×數(shù)量+乙種商品單件利潤×數(shù)量代入數(shù)據即可得出結論;
(2)設第二次乙種商品是按原價打y折銷售,根據總利潤=甲種商品單件利潤×數(shù)量+乙種商品單件利潤×數(shù)量即可得出關于y的一元一次方程,解之即可得出結論.
解答 解:(1)設第一次購進甲種商品x件,則乙的件數(shù)為($\frac{1}{2}$x+15)件,
根據題意得:20x+30($\frac{1}{2}$x+15)=5000,
解得:x=130,
∴$\frac{1}{2}$x+15=65+15=80,
(29-20)×130+(40-30)×80=1970(元).
答:兩種商品全部賣完后可獲得1970元利潤.
(2)設第二次乙種商品是按原價打y折銷售,
根據題意得:(29-20)×130+(40×$\frac{y}{10}$-30)×80×3=1970+160,
解得:y=8.5.
答:第二次乙種商品是按原價打8.5折銷售.
點評 本題考查了一元一次方程的應用,解題的關鍵是:(1)根據數(shù)量關系總進價=甲種商品單件進價×數(shù)量+乙種商品單件進價×數(shù)量列出關于x的一元一次方程;(2)根據數(shù)量關系總利潤=甲種商品單件利潤×數(shù)量+乙種商品單件利潤×數(shù)量列出關于y的一元一次方程.本題屬于中檔題,難度不大,正確的列出方程才能更好的解決問題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數(shù)學 來源: 題型:解答題
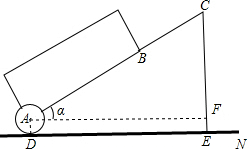 拉桿箱是人們出行的必需品,采用拉桿箱可以讓我們的出行更輕松,如圖,已知某種拉桿箱箱體長AB=50cm,拉桿最大伸長距離BC=40cm,點A到地面的距離AD=8cm,拉桿箱與水平面的夾角α的度數(shù)為35°.(提示:sin35°≈0.57,cos35°≈0.82).
拉桿箱是人們出行的必需品,采用拉桿箱可以讓我們的出行更輕松,如圖,已知某種拉桿箱箱體長AB=50cm,拉桿最大伸長距離BC=40cm,點A到地面的距離AD=8cm,拉桿箱與水平面的夾角α的度數(shù)為35°.(提示:sin35°≈0.57,cos35°≈0.82).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| 信件質量p(克) | 0<p≤20 | 20<p≤40 | 40<x≤60 |
| 郵資q(元) | 1.20 | 2.40 | 3.60 |
| A. | ①④ | B. | ①③ | C. | ③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com