
 如圖,在正方形ABCD中,F是對角線AC上任一點,BF⊥EF,AD=1.
如圖,在正方形ABCD中,F是對角線AC上任一點,BF⊥EF,AD=1.分析 (1)如圖1中,作FM⊥AD于M,FN⊥AB于N.只要證明△FME≌△FNB即可.
(2)如圖2中,GF的長度是一個定值.連接BD交AC于O.首先求出OB的長,再證明△EGF≌△FOB,即可推出FG=OB=$\frac{\sqrt{2}}{2}$.
解答 (1)證明:如圖1中,作FM⊥AD于M,FN⊥AB于N.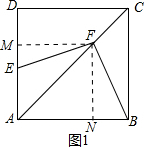
∵四邊形ABCD是正方形,
∴∠CAD=∠CAB=45°,
∴FN=FM,
∵∠FMA=∠MAN=∠FNA=90°,
∴∠MFN=∠EFB=90°,
∴∠MFE=∠NFB,
在△FME和△FNB中,
$\left\{\begin{array}{l}{∠FME=∠FNB}\\{FM=FN}\\{∠MEE=∠NFB}\end{array}\right.$,
∴△FME≌△FNB,
∴EF=FB.
(2)如圖2中,GF的長度是一個定值.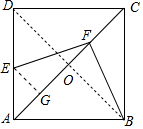
理由:連接BD交AC于O.
∵四邊形ABCD是正方形,
∴AD=AB=BC=CD=1,BD=$\sqrt{2}$,OB=OD=$\frac{\sqrt{2}}{2}$,AC⊥BD,
∴∠EFB=∠BOF=∠EGF=90°,
∵∠EFG+∠FEG=90°,∠EFG+∠BFO=90°,
∴∠FEO=∠BFO,
在△EGF和△FOB中,
$\left\{\begin{array}{l}{∠EGF=∠FOB}\\{∠FEG=∠BFO}\\{EF=FB}\end{array}\right.$,
∴△EGF≌△FOB,
∴FG=OB=$\frac{\sqrt{2}}{2}$,
∴FG的長度是定值.
點評 本題考查正方形的性質、全等三角形的判定和性質、勾股定理等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形解決問題,屬于中考常考題型.


科目:初中數學 來源: 題型:填空題
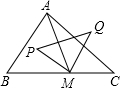 如圖,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是邊BC上一動點,P、Q分別是△ABM、△ACM外接圓的圓心,則S△PMQ的最小值為6$\sqrt{3}$+12.
如圖,△ABC中,∠B=60°,∠C=45°,BC=4+4$\sqrt{3}$,M是邊BC上一動點,P、Q分別是△ABM、△ACM外接圓的圓心,則S△PMQ的最小值為6$\sqrt{3}$+12.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
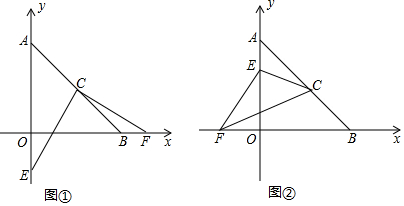
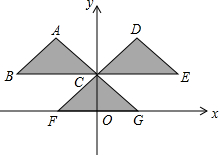 如圖,三角形CFG的頂點坐標分別為C(0,$\frac{\sqrt{2}}{2}$),F(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移兩次,構成如圖所示的圖案(其中點B、C、E在一條平行于x軸的直線上).
如圖,三角形CFG的頂點坐標分別為C(0,$\frac{\sqrt{2}}{2}$),F(-$\frac{\sqrt{2}}{2}$,0),G($\frac{\sqrt{2}}{2}$,0).把三角形CFG平移兩次,構成如圖所示的圖案(其中點B、C、E在一條平行于x軸的直線上).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3-$2\sqrt{2}$ | B. | 3+$2\sqrt{2}$ | C. | 6-4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com