
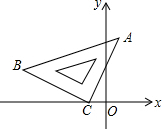
 在平面直角坐標系中,將一塊等腰三角板ABC如圖放置.已知直角頂點C的坐標為(-2,0),頂點B的坐標為(-7,3).求點A的坐標.
在平面直角坐標系中,將一塊等腰三角板ABC如圖放置.已知直角頂點C的坐標為(-2,0),頂點B的坐標為(-7,3).求點A的坐標. 分析 作AE⊥x軸于點E,作BF⊥x軸于點F,如圖,易得OC=2,OF=7,BF=3,CF=5,再根據等腰直角三角形的性質得CA=CB,∠ACB=90°,接著根據等角的余角相等得到∠CAE=∠BCF,于是利用“AAS”判斷△ACE≌△CBF,則CE=BF=3,AE=CF=5,然后根據第一象限內點的坐標特征寫出A點坐標.
解答 解:作AE⊥x軸于點E,作BF⊥x軸于點F,如圖,
∵C(-2,0),B(-7,3),
∴OC=2,OF=7,BF=3,
∴CF=OF-OC=5,
∵△ABC為等腰直角三角形,
∴CA=CB,∠ACB=90°,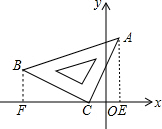
∴∠ACE+∠BCF=90°,
∵∠ACE+∠CAE=90°,
∴∠CAE=∠BCF,
在△ACE和△CBF中
$\left\{\begin{array}{l}{∠AEC=∠CFB}\\{∠CAE=∠BCF}\\{AC=CB}\end{array}\right.$,
∴△ACE≌△CBF,
∴CE=BF=3,AE=CF=5,
∴OE=CE-OC=3-2=1,
∴A點坐標為(1,5).
點評 本題考查了全等三角形的判定與性質:全等三角形的判定是結合全等三角形的性質證明線段和角相等的重要工具.在應用全等三角形的判定時,要注意三角形間的公共邊和公共角,必要時添加適當輔助線構造三角形;在應用全等三角形的性質時主要是得到對應角相等或對應線段相等.解決本題的關鍵是構建全等三角形求出點A到x軸和y軸的距離.


科目:初中數學 來源: 題型:選擇題
| A. | x2+3x+2=x(x+3)+2 | B. | 4x2-9=(4x+3)(4x-3) | C. | x2-5x+6=(x-2)(x-3) | D. | a2-2a+1=(a+1)2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 《九章算術》是中國傳統數學最重要的著作,奠定了中國傳統數學的基本框架.它的代數成就主要包括開方術、正負術和方程術.其中,方程術是《九章算術》最高的數學成就.《九2x=-6章算術》中記載:“今有人共買雞,人出九,盈十一;人出六,不足十六.問人數、雞價各幾何?”
《九章算術》是中國傳統數學最重要的著作,奠定了中國傳統數學的基本框架.它的代數成就主要包括開方術、正負術和方程術.其中,方程術是《九章算術》最高的數學成就.《九2x=-6章算術》中記載:“今有人共買雞,人出九,盈十一;人出六,不足十六.問人數、雞價各幾何?”| A. | 9x+11=6x-16 | B. | 9x-11=6x+16 | C. | $\frac{x-11}{9}=\frac{x+16}{6}$ | D. | $\frac{x+11}{9}=\frac{x-16}{6}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
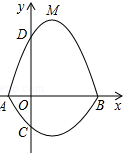 如圖,在平面直角坐標系xOy中,A、B為x軸上兩點,C、D為y軸上的兩點,經過點A、C、B的拋物線的一部分C1與經過點A、D、B的拋物線的一部分C2組合成一條封閉曲線,我們把這條封閉曲線成為“蛋線”.已知點C的坐標為(0,-$\frac{3}{2}$),點M是拋物線C2:y=mx2-2mx-3m(m<0)的頂點.
如圖,在平面直角坐標系xOy中,A、B為x軸上兩點,C、D為y軸上的兩點,經過點A、C、B的拋物線的一部分C1與經過點A、D、B的拋物線的一部分C2組合成一條封閉曲線,我們把這條封閉曲線成為“蛋線”.已知點C的坐標為(0,-$\frac{3}{2}$),點M是拋物線C2:y=mx2-2mx-3m(m<0)的頂點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
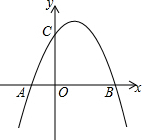 如圖,已知c>0,拋物線y=-x2+bx+c與x軸交于A(x1,0),B(x2,0)兩點(x2>x1),與y軸交于點C.
如圖,已知c>0,拋物線y=-x2+bx+c與x軸交于A(x1,0),B(x2,0)兩點(x2>x1),與y軸交于點C.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 列方程解應用題
列方程解應用題查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com