
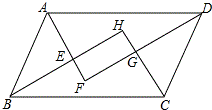
 如圖,平行四邊形ABCD的四個內角的平分線分別相交于點E、F、G、H,求證:四邊形EFGH是矩形.
如圖,平行四邊形ABCD的四個內角的平分線分別相交于點E、F、G、H,求證:四邊形EFGH是矩形. 分析 利用三個內角等于90°的四邊形是矩形,即可證明.
解答 解:結論:四邊形EFGH是矩形,
理由:∵四邊形ABCD是平行四邊形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BH,CH分別平分∠ABC與∠BCD,
∴∠HBC=$\frac{1}{2}$∠ABC,∠HCB=$\frac{1}{2}$∠BCD,
∴∠HBC+∠HCB=$\frac{1}{2}$(∠ABC+∠BCD)=$\frac{1}{2}$×180°=90°,
∴∠H=90°,
同理∠HEF=∠F=90°,
∴四邊形EFGH是矩形.
點評 本題考查了矩形的判定,平行四邊形的性質,角平分線的定義,平行線的性質,難度適中.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:選擇題
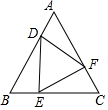 如圖,正△ABC的三邊上有三點D,E,F,且AD=BE=CF,設AB=x,DE=y,△ADF的內切圓的半徑為$\sqrt{3}$,則關于x的函數關系式為( )
如圖,正△ABC的三邊上有三點D,E,F,且AD=BE=CF,設AB=x,DE=y,△ADF的內切圓的半徑為$\sqrt{3}$,則關于x的函數關系式為( )| A. | y=x-6 | B. | y=$\frac{\sqrt{3}}{2}x$ | C. | y=x-3 | D. | y=$\frac{\sqrt{3}}{x}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
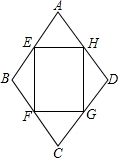 如圖,四邊形ABCD是一個菱形綠草地,其周長為40$\sqrt{2}$m,∠ABC=120°,在其內部有一個矩形花壇EFGH,其四個頂點恰好在菱形ABCD各邊中點,現準備在花壇中種植茉莉花,其單價為30元/2,則需投資資金多少元?($\sqrt{3}$取1.732)
如圖,四邊形ABCD是一個菱形綠草地,其周長為40$\sqrt{2}$m,∠ABC=120°,在其內部有一個矩形花壇EFGH,其四個頂點恰好在菱形ABCD各邊中點,現準備在花壇中種植茉莉花,其單價為30元/2,則需投資資金多少元?($\sqrt{3}$取1.732)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com