
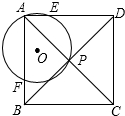
 如圖,四邊形ABCD為正方形,⊙O過正方形的頂點A和對角線的交點P,分別交AB、AD于點F、E.若⊙O的半徑為$\frac{{\sqrt{3}}}{2}$,AB=$\sqrt{2}$+1,則$\frac{AE}{ED}$的值為$\frac{\sqrt{2}}{2}$或$\sqrt{2}$.
如圖,四邊形ABCD為正方形,⊙O過正方形的頂點A和對角線的交點P,分別交AB、AD于點F、E.若⊙O的半徑為$\frac{{\sqrt{3}}}{2}$,AB=$\sqrt{2}$+1,則$\frac{AE}{ED}$的值為$\frac{\sqrt{2}}{2}$或$\sqrt{2}$. 分析 連EF,由∠BAD=90°,得到EF為⊙O的直徑,即EF=$\sqrt{3}$,所以AF2+AE2=EF2=($\sqrt{3}$)2=3,而DE=AF,所以DE2+AE2=EF2=($\sqrt{3}$)2=3;由AD=AE+ED=AB=$\sqrt{2}$,這樣得到關于DE,AE的方程組,解方程組求出DE,AE,即可得到$\frac{AE}{ED}$的值.
解答 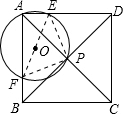 解:連EF,
解:連EF,
∵∠BAD=90°,
∴EF為⊙O的直徑,
而⊙O的半徑為$\frac{\sqrt{3}}{2}$,
∴EF=$\sqrt{3}$,
∴AF2+AE2=EF2=($\sqrt{3}$)2=3①,
而DE=AF,
DE2+AE2=3;
又∵AD=AE+ED=AB,
∴AE+ED=$\sqrt{2}$②,
由①②聯立起來組成方程組,解之得:AE=1,ED=$\sqrt{2}$或AE=$\sqrt{2}$,ED=1,
∴$\frac{AE}{ED}$的值為$\frac{\sqrt{2}}{2}$或$\sqrt{2}$.
故答案為:$\frac{\sqrt{2}}{2}$或$\sqrt{2}$.
點評 本題考查了圓周角定理.在同圓或等圓中,同弧和等弧所對的圓周角相等,一條弧所對的圓周角是它所對的圓心角的一半.同時考查了直徑所對的圓周角為直角、圓內接四邊形的性質、正方形的性質以及方程組的解法.


 習題精選系列答案
習題精選系列答案科目:初中數學 來源: 題型:選擇題
 如圖,己知AB=AD.下列條件中,不能作為判定△ABC≌△ADC條件的是( )
如圖,己知AB=AD.下列條件中,不能作為判定△ABC≌△ADC條件的是( )| A. | .BC=DC | B. | .∠BAC=∠DAC | C. | .∠B=∠D=90° | D. | .∠ACB=∠ACD |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 由x=y,得到x+2=y+2 | B. | 由2a-3=b-3,得到2a=b | ||
| C. | 由m=n,得到2am=2an | D. | 由am=an,得到m=n |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 相離 | B. | 相切 | C. | 相交 | D. | 不能確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| 品牌 | 月租費 | 本地話費(元/分鐘) | 長途話費(元/分鐘) |
| 全球通 | 13元 | 0.35 | 0.15 |
| 神州行 | 0元 | 0.60 | 0.30 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 工序 時間 模型 | 打磨(A組) | 組裝(B組) |
| 模型甲 | 9分鐘 | 5分鐘 |
| 模型乙 | 6分鐘 | 11分鐘 |
| A. | 20分鐘 | B. | 22分鐘 | C. | 26分鐘 | D. | 31分鐘 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com