
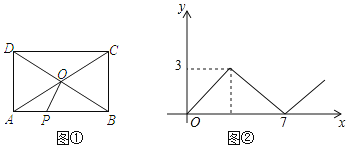
【題目】如圖①,在矩形ABCD中,AB>AD,對角線AC、BD相交于點O,動點P由點A出發,沿AB→BC→CD向點D運動,設點P的運動路徑為x,△AOP的面積為y,圖②是y關于x的函數關系圖象,則AB邊的長為( )
A. 3B. 4C. 5D. 6
【答案】B
【解析】
根據圖形,分情況當P點在AB上運動時,△AOP面積逐漸增大,當P點到達B點時,△AOP面積最大為3,推出ABBC=12;當P點在BC上運動時,△AOP面積逐漸減小,當P點到達C點時,△AOP面積為0,此時結合圖象可知P點運動路徑長為7,可推出AB.
解:當P點在AB上運動時,△AOP面積逐漸增大,當P點到達B點時,△AOP面積最大為3.
∴![]() AB
AB![]() BC=3,即ABBC=12.
BC=3,即ABBC=12.
當P點在BC上運動時,△AOP面積逐漸減小,當P點到達C點時,△AOP面積為0,此時結合圖象可知P點運動路徑長為7,
∴AB+BC=7.
則BC=7﹣AB,代入ABBC=12,得AB2﹣7AB+12=0,解得AB=4或3,
因為AB>BC,所以AB=4.
故選:B.


 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:初中數學 來源: 題型:
【題目】“六一”兒童節,某玩具超市設立了一個如圖所示的可以自由轉動的轉盤,開展有獎購買活動.顧客購買玩具就能獲得一次轉動轉盤的機會,當轉盤停止時,指針落在哪一區域就可以獲得相應獎品.下表是該活動的一組統計數據.下列說法:①當n很大時,估計指針落在“鉛筆”區域的頻率大約是0.70;②假如你去轉動轉盤一次,獲得鉛筆的概率大約是0.70;③如果轉動轉盤2000次,指針落在“文具盒”區域的次數大約有600次;④轉動轉盤10次,一定有3次獲得文具盒.中正確的是_____
轉動轉盤的次數n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“鉛筆”區域的次數m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“鉛筆”區域的頻率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD繞其右下角的頂點按順時針方向旋轉90°至圖①位置,繼續繞右下角的頂點按順時針方向旋轉90°至圖②位置,以此類推,這樣連續旋轉2017次.若AB=4,AD=3,則頂點A在整個旋轉過程中所經過的路徑總長為( )

A. 2017π B. 2034π C. 3024π D. 3026π
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=kx+b與雙曲線![]() (x﹤0)相交于A(-4,a)、B(-1,4)兩點.
(x﹤0)相交于A(-4,a)、B(-1,4)兩點.

(1)求直線和雙曲線的解析式;
(2)在y軸上存在一點P,使得PA+PB的值最小,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
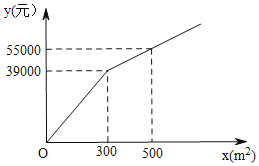
【題目】為了美化環境,建設宜居衡陽,我市準備在一個廣場上種植甲、乙兩種花卉.經市場調查,甲種花卉的種植費用y(元)與種植面積x(m2)之間的函數關系如圖所示,乙種花卉的種植費用為每平方米100元.
(1)求y與x的函數關系式;
(2)廣場上甲、乙兩種花卉的種植面積共1000m2,若甲種花卉的種植面積不少于200m2,且不超過乙種花卉種植面積的3倍,那么應該怎忙分配甲、乙兩種花卉的種植面積才能使種植費用最少?最少總費用為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
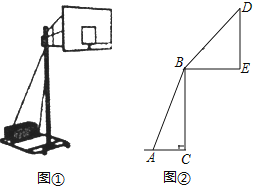
【題目】如圖①,②分別是某款籃球架的實物圖和示意圖,已知支架AB的長為2.3m,支架AB與地面的夾角∠BAC=70°,BE的長為1.5m,籃板部支架BD與水平支架BE的夾角為46°,BC、DE垂直于地面,求籃板頂端D到地面的距離.(結果保留一位小數,參考數據:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】父親節即將到來之際,某商店準備購進![]() 、
、![]() 兩種男裝進行銷售,其中每套
兩種男裝進行銷售,其中每套![]() 種男裝的進價比每套
種男裝的進價比每套![]() 種男裝的進價多
種男裝的進價多![]() 元用
元用![]() 元購進
元購進![]() 種男裝的數量是用
種男裝的數量是用![]() 元購進
元購進![]() 種男裝數量的
種男裝數量的![]() 倍.
倍.
(1)求每套![]() 種男裝和每套
種男裝和每套![]() 種男裝的進價各是多少元:
種男裝的進價各是多少元:
(2)若該商店本次購進![]() 種男裝的數量比購進
種男裝的數量比購進![]() 種男裝的數量的
種男裝的數量的![]() 倍還多
倍還多![]() 套,該商店每套
套,該商店每套![]() 種男裝的銷售價格為
種男裝的銷售價格為![]() 元,每套
元,每套![]() 種男裝的銷售價格為
種男裝的銷售價格為![]() 元,若將本次購進的
元,若將本次購進的![]() 、
、![]() 兩種男裝全部售出后獲得的利潤不少于
兩種男裝全部售出后獲得的利潤不少于![]() 元,那么該商店至少需要購進
元,那么該商店至少需要購進![]() 種男裝多少套?
種男裝多少套?
查看答案和解析>>
科目:初中數學 來源: 題型:
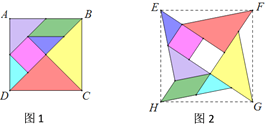
【題目】七巧板是我們祖先的一項卓越創造,被西方人譽為“東方魔板”.下面的兩幅圖正方形(如圖1)、“風車型”(如圖2)都是由同一副七巧板拼成的,則圖中正方形ABCD,EFGH的面積比為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
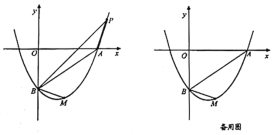
【題目】若二次函數![]() 的圖象與
的圖象與![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,且過點
,且過點![]() .
.
(1)求二次函數表達式;
(2)若點![]() 為拋物線上第一象限內的點,且
為拋物線上第一象限內的點,且![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)在拋物線上(![]() 下方)是否存在點
下方)是否存在點![]() ,使
,使![]() ?若存在,求出點
?若存在,求出點![]() 到
到![]() 軸的距離;若不存在,請說明理由.
軸的距離;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com