

分析 根據(jù)勾股定理求出斜邊AB,(1)當(dāng)AB=AD時(shí),求出CD即可;(2)當(dāng)AB=BD時(shí),求出CD、AD即可;(3)當(dāng)DA=DB時(shí),設(shè)AD=x,則CD=x-6,求出即可.
解答 解:
在Rt△ABC中,∵∠ACB=90°,AC=8m,BC=6m,
∴AB=10m,
(1)如圖1,當(dāng)AB=AD時(shí),CD=6m,
則△ABD的面積為:$\frac{1}{2}$BD•AC=$\frac{1}{2}$×(6+6)×8=48(m2);
(2)如圖2,當(dāng)AB=BD時(shí),CD=4m,則△ABD的面積為:$\frac{1}{2}$BD•AC=$\frac{1}{2}$×(6+4)×8=40(m2);
(3)如圖3,當(dāng)DA=DB時(shí),設(shè)AD=x,則CD=x-6,
則x2=(x-6)2+82,
∴x=$\frac{25}{3}$,
則△ABD的面積為:$\frac{1}{2}$BD•AC=$\frac{1}{2}$×$\frac{25}{3}$×8=$\frac{100}{3}$(m2);
答:擴(kuò)充后等腰三角形綠地的面積是48m2或40m2或$\frac{100}{3}$m2.
點(diǎn)評(píng) 本題主要考查對(duì)勾股定理,等腰三角形的性質(zhì)等知識(shí)點(diǎn)的理解和掌握,能通過(guò)分類(lèi)求出等腰三角形的所有情況是解此題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 1個(gè) | B. | 2個(gè) | C. | 3個(gè) | D. | 4個(gè) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | W=20x+16800≥17560 | B. | y=(x+1)2+2 | ||
| C. | y=(x-1)2-2 | D. | y=(x+1)2-2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | (-3,-2) | B. | (3,-2) | C. | (-3,2) | D. | (3,2) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
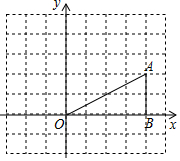 如圖,在平面直角坐標(biāo)系中,已知點(diǎn)A(4,2),B(4,0).
如圖,在平面直角坐標(biāo)系中,已知點(diǎn)A(4,2),B(4,0).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com