

分析 ①運用軸對稱的性質作出B的對稱點C,連接AC與a交于點M,M就是抽水站的位置.及三角形的三邊關系【假設N點(不與點M重合)即是所求,而AN+NC>AM+BM,所以假設不成立】解決第一個問題;
②作出角平分線(∠AOB的角平分線)和線段垂直平分線(MN的垂直平分線)交于點P,利用它們的性質來解決第二問.
解答 解:①如圖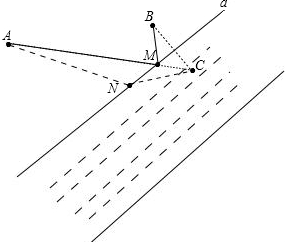
作出B的對稱點C,連接AC與a交于點M,M就是抽水站的位置.
假設N點(不與點M重合)即是所求,而AN+NC>AM+BM,所以假設不成立.
點M即是所求抽水站的位置.
②如圖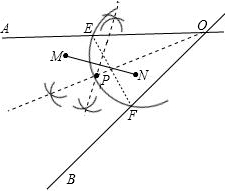
作出∠AOB的角平分線與MN的垂直平分線交于點P,P點就是所求的物資倉庫.
點評 此題主要考查了基本作圖的作法--畫角平分線與作對稱點,關鍵是熟練掌握基本作圖的方法.


科目:初中數學 來源:2016-2017學年北京市西城區七年級上學期期末考試數學試卷(解析版) 題型:解答題
閱讀下列材料:
《張丘建算經》是一部數學問題集,其內容、范圍與《九章算術》相仿。其中提出并解決了一個在數學史上非常著名的不定方程問題,通常稱為“百雞問題”:“今有雞翁一值錢五,雞母一值錢三,雞雛三值錢一。凡百錢買雞百只,問雞翁、母、雛各幾何。”

譯文:公雞每只值五文錢,母雞每只值三文錢,小雞每三只值一文錢。現在用一百文錢買一百只雞,問這一百只雞中,公雞、母雞、小雞各有多少只?
結合你學過的知識,解決下列問題:
(1)若設公雞有x只,母雞有y只,
①則小雞有____________只,買小雞一共花費____________文錢;(用含x,y的式子表示)
②根據題意列出一個含有x,y的方程: ______________________________;
(2)若對“百雞問題”增加一個條件:公雞數量是母雞數量的3倍,求此時公雞、母雞、小雞各有多少只?
(3)除了問題(2)中的解之外,請你再直接寫出兩組符合“百雞問題”的解。
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | a2 | C. | -a | D. | $\frac{1}{a^2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
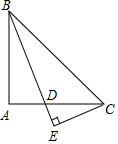 已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于點D,CE垂直于BD,交BD的延長線于點E,求證:BD=2CE.
已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于點D,CE垂直于BD,交BD的延長線于點E,求證:BD=2CE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
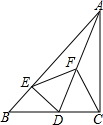 如圖,在Rt△ABC中,∠ACB=90°,D是邊BC上一動點(不與B,C重合),DE⊥AB于點E,點F是線段AD的中點,連接EF,CF.
如圖,在Rt△ABC中,∠ACB=90°,D是邊BC上一動點(不與B,C重合),DE⊥AB于點E,點F是線段AD的中點,連接EF,CF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
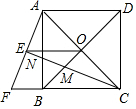 如圖,正方形ABCD的對角線AC,BD相交于點O,延長CB至點F,使CF=CA,連接AF,∠ACF的平分線分別交AF,AB,BD于點E,N,M,連接EO.
如圖,正方形ABCD的對角線AC,BD相交于點O,延長CB至點F,使CF=CA,連接AF,∠ACF的平分線分別交AF,AB,BD于點E,N,M,連接EO.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 固定費用(元) | 免費撥打時間(分鐘) | 超出免費時間后單價(元/分鐘) | |
| A | 18 | 1500 | 0.1 |
| B | 38 | 4000 | 0.07 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com