
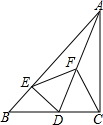
 如圖,在Rt△ABC中,∠ACB=90°,D是邊BC上一動點(不與B,C重合),DE⊥AB于點E,點F是線段AD的中點,連接EF,CF.
如圖,在Rt△ABC中,∠ACB=90°,D是邊BC上一動點(不與B,C重合),DE⊥AB于點E,點F是線段AD的中點,連接EF,CF.分析 (1)EF和CF分別是直角△AED和直角△ACD斜邊上的中線,依據直角三角形斜邊上的中線等于斜邊的一半即可證得;
(2)證明△EFC是等邊三角形,然后根據等邊三角形的定義以及直角三角形的性質求解.
解答  解:(1)EF=CF,
解:(1)EF=CF,
在Rt△AED和Rt△ACD中,
∵點F是線段AD的中點,
∴EF=$\frac{1}{2}$ AD,CF=$\frac{1}{2}$AD,
∴EF=CF.
(2)由(1)可知EF=AF=CF,
∴∠AEF=∠EAF,∠ACF=∠CAF,
∴∠EFD=2∠EAF,∠CFD=2∠CAF,
∴∠EFC=2∠BAC=60°,
又EF=CF,
∴△EFC為等邊三角形,
∴CE=EF=$\frac{1}{2}$ AD.
點評 本題考查了直角三角形斜邊上的中線等于斜邊的一半以及等邊三角形的判定與性質,證得△EFC是等邊三角形是關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:2017屆江蘇省無錫市九年級下學期第一次模擬考試數學試卷(解析版) 題型:單選題
下圖是由幾個小立方塊搭成的幾何體的俯視圖,小正方形中的數字表示在該位置的小立方塊的個數,那么這個幾何體的主視圖是( )
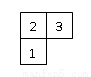
A. 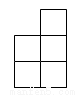 B.
B.  C.
C. 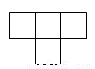 D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
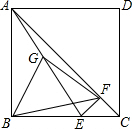 在正方形ABCD中.
在正方形ABCD中.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 時間/t(min) | 1 | 2.5 | 5 | 10 | 20 | 50 | … |
| 路程/s(km) | 2 | 5 | 10 | 20 | 40 | 100 | … |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com