
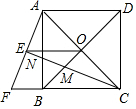
 如圖,正方形ABCD的對角線AC,BD相交于點(diǎn)O,延長CB至點(diǎn)F,使CF=CA,連接AF,∠ACF的平分線分別交AF,AB,BD于點(diǎn)E,N,M,連接EO.
如圖,正方形ABCD的對角線AC,BD相交于點(diǎn)O,延長CB至點(diǎn)F,使CF=CA,連接AF,∠ACF的平分線分別交AF,AB,BD于點(diǎn)E,N,M,連接EO.分析 (1)利用正方形的性質(zhì)和勾股定理計(jì)算即可;
(2)證明方法一、先判斷出EO為△AFC的中位線,再由EO∥BC得出$\frac{OE}{BC}=\frac{EM}{CM}$,進(jìn)而利用直角三角形得出CM=$\sqrt{2}$EM,再判斷出△CBN∽△COM得出比例式,進(jìn)而得出CN=$\sqrt{2}$CM,即可得出結(jié)論.
證明方法二、先判斷出∠OEC=∠OCE,再判斷出∠NBC=∠COM=90°,進(jìn)而得出△CBN∽△COM,即可得出結(jié)論.
解答 解:(1)∵四邊形ABCD是正方形,
∴△ABD是等腰直角三角形,
∴2AB2=BD2,
∵BD=$\sqrt{2}$,
∴AB=1,
∴正方形ABCD的邊長為1;
(2)CN=2EM
證明方法一、理由:∵四邊形ABCD是正方形,
∴AC⊥BD,OA=OC
∵CF=CA,AF是∠ACF的平分線,
∴CE⊥AF,AE=FE
∴EO為△AFC的中位線
∴EO∥BC
∴$\frac{OE}{BC}=\frac{EM}{CM}$
∴在Rt△AEN中,OA=OC
∴EO=OC=$\frac{1}{2}$AC,
$\frac{OC}{BC}=\frac{EM}{CM}=\frac{1}{\sqrt{2}}$
∴CM=$\sqrt{2}$EM
∵CE平分∠ACF,
∴∠OCM=∠BCN,
∵∠NBC=∠COM=90°,
∴△CBN∽△COM,
∴$\frac{CM}{CN}=\frac{OC}{BC}=\frac{1}{\sqrt{2}}$,
∴CN=$\sqrt{2}$CM,
即CN=2EM.
證明方法二、∵四邊形ABCD是正方形,
∴∠BAC=45°=∠DBC,
由(1)知,在Rt△ACE中,EO=$\frac{1}{2}$AC=CO,
∴∠OEC=∠OCE,
∵CE平分∠ACF,
∴∠OCE=∠ECB=∠OEC,
∴EO∥BC,
∴∠EOM=∠DBC=45°,
∵∠OEM=∠OCE
∴△EOM∽△CAN,
∴$\frac{EM}{CN}=\frac{EO}{CA}=\frac{1}{2}$,
∴CN=2CM.
點(diǎn)評 此題主要考查了相似三角形的判斷和性質(zhì),三角形的中位線,角平分線的定義,利用比例式判斷出CM=$\sqrt{2}$EM和CN=$\sqrt{2}$CM是解本題的關(guān)鍵.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源:2016-2017學(xué)年北京市西城區(qū)七年級上學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:填空題
如圖,點(diǎn)C在射線OA上,CE平分∠ACD. OF平分∠COB并與射線CD交于點(diǎn)F。

(1)依題意補(bǔ)全圖形;
(2)若∠COB+∠OCD=180°,求證:∠ACE=∠COF。
請將下面的證明過程補(bǔ)充完整。
證明:∵CE平分∠ACD,OF平分∠COB,
∴∠ACE=______________,∠COF= ∠COB。
∠COB。
(理由: _____________________________________)
∵點(diǎn)C在射線OA上,
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°,
∴∠ACD=∠____________。
(理由: ___________________________________)
∴∠ACE=∠COF。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等邊三角形 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
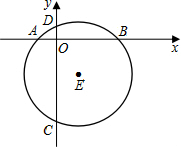 如圖,在直角坐標(biāo)系中,⊙E的半徑為5,點(diǎn)E(1,-4).
如圖,在直角坐標(biāo)系中,⊙E的半徑為5,點(diǎn)E(1,-4).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | x•x2=x2 | B. | (x5)3=x8 | C. | x6÷x2=x3 | D. | (ab)3=a3b3 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com