如圖，點C在射線OA上，CE平分∠ACD. OF平分∠COB并與射線CD交于點F。
（1）依題意補全圖形；
（2）若∠COB+∠OCD=180°，求證：∠ACE=∠COF。
請將下面的證明過程補充完整。
證明：∵CE平分∠ACD，OF平分∠COB，
∴∠ACE=______________，∠COF=
∠COB。
（理由： _____________________________________）
∵點C在射線OA上，
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°，
∴∠ACD=∠____________。
（理由： ___________________________________）
∴∠ACE=∠COF。
沖刺100分單元優化練考卷系列答案科目：初中數學 來源： 題型：填空題
查看答案和解析>>
科目：初中數學 來源：2017屆江蘇省無錫市九年級下學期第一次模擬考試數學試卷（解析版） 題型：判斷題
如圖，四邊形ABCD 內接于⊙O，BD是⊙O的直徑，過點A作⊙O的切線AE交CD的延長線于點E，DA平分∠BDE．
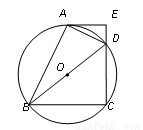
（1）求證：AE⊥CD；
（2）已知AE＝4cm，CD＝6cm，求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源：2017屆江蘇省無錫市九年級下學期第一次模擬考試數學試卷（解析版） 題型：單選題
下列命題中，假命題是（ ）
A. 經過兩點有且只有一條直線 B. 平行四邊形的對角線相等
C. 兩腰相等的梯形叫做等腰梯形 D. 圓的切線垂直于經過切點的半徑
查看答案和解析>>
科目：初中數學 來源：2016-2017學年北京市西城區七年級上學期期末考試數學試卷（解析版） 題型：解答題
閱讀下列材料：
《張丘建算經》是一部數學問題集，其內容、范圍與《九章算術》相仿。其中提出并解決了一個在數學史上非常著名的不定方程問題，通常稱為“百雞問題”：“今有雞翁一值錢五，雞母一值錢三，雞雛三值錢一。凡百錢買雞百只，問雞翁、母、雛各幾何。”
譯文：公雞每只值五文錢，母雞每只值三文錢，小雞每三只值一文錢。現在用一百文錢買一百只雞，問這一百只雞中，公雞、母雞、小雞各有多少只?
結合你學過的知識，解決下列問題：
（1）若設公雞有x只，母雞有y只，
①則小雞有____________只，買小雞一共花費____________文錢；（用含x，y的式子表示）
②根據題意列出一個含有x，y的方程： ______________________________；
（2）若對“百雞問題”增加一個條件：公雞數量是母雞數量的3倍，求此時公雞、母雞、小雞各有多少只?
（3）除了問題（2）中的解之外，請你再直接寫出兩組符合“百雞問題”的解。
查看答案和解析>>
科目：初中數學 來源： 題型：填空題
| 購票人數 | 1-30人 | 31-60人 | 60人以上 |
| 票價 | 無折扣 | 超出30人的部分，票價打八折 | 超出60人的部分，票價打五折 |
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
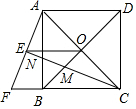如圖，正方形ABCD的對角線AC，BD相交于點O，延長CB至點F，使CF=CA，連接AF，∠ACF的平分線分別交AF，AB，BD于點E，N，M，連接EO．查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
-
-
）