
分析 (1)先根據完全平方公式和平方差公式展開,再去括號、合并可得;
(2)先將分母因式分解,計算括號內異分母分式加減,再計算除法即可得.
解答 解:(1)原式=x2+4xy+4y2-(x2-4y2)
=x2+4xy+4y2-x2+4y2
=4xy+8y2;
(2)原式=$\frac{x}{(x+3)(x-3)}$÷$\frac{2x-6-x-3-{x}^{2}+9}{(x+3)(x-3)}$
=$\frac{x}{(x+3)(x-3)}$•$\frac{(x+3)(x-3)}{x(1-x)}$
=$\frac{1}{1-x}$.
點評 本題主要考查分式的化簡和整式的化簡,熟練掌握完全平方公式和平方差公式及分式的混合運算順序、法則是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | y=-3(x+1)2-3 | B. | y=-3(x-1)2-3 | C. | y=-3(x+1)2+3 | D. | y=-3(x-1)2+3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
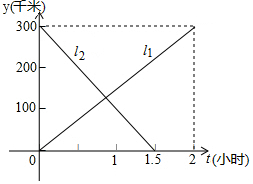 廈深鐵路開通后,直線l1與l2分別表示從深圳北開往潮陽站的動車和從潮陽站開往深圳的高鐵,兩車同時出發,設動車離深圳北的距離為y1(千米),高鐵離深圳的距離為距離y2(千米),行駛時間為t(小時),與t的函數關系如圖所示:
廈深鐵路開通后,直線l1與l2分別表示從深圳北開往潮陽站的動車和從潮陽站開往深圳的高鐵,兩車同時出發,設動車離深圳北的距離為y1(千米),高鐵離深圳的距離為距離y2(千米),行駛時間為t(小時),與t的函數關系如圖所示:查看答案和解析>>
科目:初中數學 來源: 題型:填空題
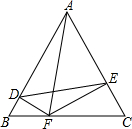 如圖,△ABC是邊長為8的等邊三角形,F是邊BC上的動點,且DF⊥AB,EF⊥AC.則四邊形ADFE的面積最大值是12$\sqrt{3}$.
如圖,△ABC是邊長為8的等邊三角形,F是邊BC上的動點,且DF⊥AB,EF⊥AC.則四邊形ADFE的面積最大值是12$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知線段AB上有兩點C、D,且AC=BD,M,N分別是線段AC,AD的中點,若AB=acm,AC=BD=bcm,且a、b滿足(a-10)2+|$\frac{b}{2}$-4|=0.
如圖,已知線段AB上有兩點C、D,且AC=BD,M,N分別是線段AC,AD的中點,若AB=acm,AC=BD=bcm,且a、b滿足(a-10)2+|$\frac{b}{2}$-4|=0.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com