
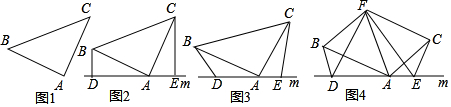
分析 (1)①分兩種證明,Ⅰ、根據BD⊥直線m,CE⊥直線m得∠BDA=∠CEA=90°,而∠BAC=90°,根據等角的余角相等得∠CAE=∠ABD,然后根據“AAS”可判斷△ADB≌△CEA,則AE=BD,AD=CE,即可得出結論;Ⅱ、同Ⅰ的方法即可.
②根據BD⊥直線m,CE⊥直線m得∠BDA=∠CEA=90°,而∠BAC=90°,根據等角的余角相等得∠CAE=∠ABD,然后根據“AAS”可判斷△ADB≌△CEA,則AE=BD,AD=CE,于是DE=AE+AD=BD+CE;
(2)利用∠BDA=∠BAC=α,則∠DBA+∠BAD=∠BAD+∠CAE=180°-α,得出∠CAE=∠ABD,進而得出△ADB≌△CEA即可得出答案;
(3)由△ABF和△ACF均為等邊三角形,得到BAC=∠BAF+∠CAF=120°,利用∠BDA=∠BAC=120°,則∠DBA+∠BAD=∠BAD+∠CAE=60°,得出∠CAE=∠ABD,進而得出△ADB≌△CEA,根據全等三角形的性質得到AE=BD,∠ABD=∠CAE,得到∠DBF=∠FAE,根據全等三角形的性質得到DF=EF,∠BFD=∠AFE,根據得到結論
解答 證明:(1)①Ⅰ、如圖1,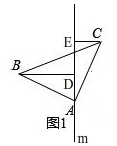 ②∵BD⊥直線m,CE⊥直線m,
②∵BD⊥直線m,CE⊥直線m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠BDA=∠CEA}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE-AD=BD-CE;
Ⅱ、如圖1-1,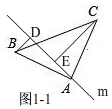
∵BD⊥直線m,CE⊥直線m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠BDA=∠CEA}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AD-AE=CE-BD,
綜上兩種情況:DE=|BD-CE|,
故答案為:①=,②DE=BD+CE;
②∵BD⊥直線m,CE⊥直線m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠BDA=∠CEA}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠BDA=∠CEA}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3)∵△ABF和△ACF均為等邊三角形,
∴BAC=∠BAF+∠CAF=120°,
∴∠BDA=∠BAC=120°,
∴∠DBA+∠BAD=∠BAD+∠CAE=60°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠BDA=∠CEA}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△CEA(AAS),
∴AE=BD,∠ABD=∠CAE,
∵∠DBF=60°+∠ABD,∠FAE=60°+∠CAE,
∴∠DBF=∠FAE,
在△BDF與△AEF中,$\left\{\begin{array}{l}{BD=AE}\\{∠DBF=∠EAF}\\{BF=AF}\end{array}\right.$,
∴△BDF≌△AEF,
∴DF=EF,∠BFD=∠AFE,
∵∠BFD+∠AFD=60°,
∴∠EFA+∠AFD=60°,
即∠DFE=60°,
∴△DEF是等邊三角形,
∴△DEF的周長為3DE=3a.
點評 此題是三角形綜合題,主要考查全等三角形的判定和性質,等邊三角形的性質,由條件證明三角形全等得到BD=AE、CE=AD是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
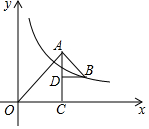 如圖,點C在x軸的正半釉上,且∠ACO=90°,CO=CA,點D在邊AC上,在邊AC的右側取一點B,使∠ADB=90°,且BD=DA,反比例函數y=$\frac{k}{x}$在第一象限的圖象經過點B,若S△OAC-S△BAD=5k-2,則k的值為$\frac{4}{9}$.
如圖,點C在x軸的正半釉上,且∠ACO=90°,CO=CA,點D在邊AC上,在邊AC的右側取一點B,使∠ADB=90°,且BD=DA,反比例函數y=$\frac{k}{x}$在第一象限的圖象經過點B,若S△OAC-S△BAD=5k-2,則k的值為$\frac{4}{9}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
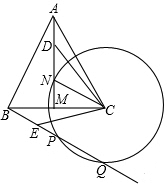 如圖,在等邊△ABC中,已知AB=8cm,線段AM為BC邊上的中線.點N在線段AM上,且MN=3cm,動點D在直線AM上運動,連接CD,△CBE是由△CAD旋轉得到的.以點C為圓心,以CN為半徑作⊙C與直線BE相交于點P,Q兩點.
如圖,在等邊△ABC中,已知AB=8cm,線段AM為BC邊上的中線.點N在線段AM上,且MN=3cm,動點D在直線AM上運動,連接CD,△CBE是由△CAD旋轉得到的.以點C為圓心,以CN為半徑作⊙C與直線BE相交于點P,Q兩點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com